\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
Math and science::Algebra::Aluffi

Identity, inclusion and restriction

This note describes 3 concepts: identity functions, inclusion functions and function restriction.

Identity function

Every set \( A \) has a function whose graph is the subset of \(A \times A \) consisting of the elements on the diagonal. This function is called the identity function on \( A \), denoted as \( \operatorname{id_A} \).

\[ \operatorname{id_A} : A \to A, \quad \forall a \in A, \, \operatorname{id_A}(a) = a \]

The identity function can be generalized slightly to arrive at the inclusion function.

Inclusion function

Let \( S \) be a subset of \( A \). The inclusion function \( i : S \to A \) maps an element in \( S \) to the same elements in \( A \).

\[ i : S \to A, \quad \forall s \in S, \, i(s) = s \]

For a given function \( f \), the inclusion function composes with \( f \) to create a restriction.

Restriction

Let \( f : A \to X \) be a function, and let \( S \subseteq A \) be a subset of \( A \). The restriction of \( f \) to \( S \), denoted as \( f|_{S} \) is defined as:

\[ f|_{S} : S \to X, \quad \forall s \in S, \, f|_{S} = f(s) \]

The restriction \( f|_{S} \) can be viewed as the composition \( f \circ i \), where \( i : S \to A \) is the inclusion function.


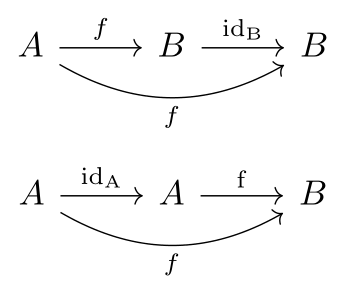
Identity function and composition

The identity function is very special with respect to composition: for any function \( f \), both \( \operatorname{id_B} \circ f = f \) and \(f \circ \operatorname{id_A} = f \). As a graphical representation, these two statements correspond to stating that the following two diagrams compute.

Source

Aluffi
p9