\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Answer
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
Math and science::Algebra::Aluffi

Injectivity and surjectivity

Injective

A function \( f : A \to B \) is injective iff

[\[ (\forall a' \in A)(\forall a'' \in A) \quad ? \]]

Injections are often denoted like [\( A \quad ? \quad B \)].

Surjective

A function \( f : A \to B \) is surjective iff

[\[ (\forall b \in B) (\exists a \in A) \quad ? \]]

Surjections are often denoted like [\( A \quad ? \quad B \)].

Bijective

A function \( f \) that is both injective and surjective is said to be bijective. A bijective function is called a bijection or a one-to-one correspondence or an isomorphism of sets; it is is often denoted like \( f : A \xrightarrow{\sim} B \).

If there is a bijection between sets \( A \) and \( B \), then each element \( a \) of \( A \) can be matched with exactly one element \( b \) of \( B \). \( A \) and \( B \) are said to be [...]. The statement that \( A \) and \( B \) have such a relationship is often denoted as \( A \cong B \).

From the perspective of inverses

If \( f : A \to B \) is a bijection, it can be 'flipped' to define a function \( g : B \to A \). This is a flipping of \( \Gamma_f \), the graph of \( f \), along it's diagonal. \( f \) being a bijection insures that such a flipping action produces a valid function. The function \( g \) has two interesting properties:

[\[ g \circ f = \quad ? \]]
[\[ f \circ g = \quad ? \]]

These properties correspond to the statement that the following two diagrams compute:

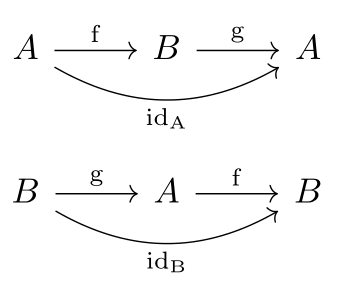
Bijections have inverses

The first identity above states that \( g \) is a [...]-inverse of \( f \). The second identity states that \( g \) is a [...]-inverse of \( f \). Combined we say that \( g \) is the inverse of \( f \), and denote it as [...]. Thus, bijections have inverses.

If a function has an inverse, is it a bijection?

This is [true or false?]. We can, in fact, break this statement into two pieces.

Let \( A \) and \( B \) be sets, with \( A \neq \emptyset \), and let \( f : A \to B \) be a function. Then the following bi-implications hold:

  1. \( f \) has a left-inverse if and only if it is [...].
  2. \( f \) has a right-inverse if and only if it is [...].

Can you think of the proof of these two bi-implications?

Futhermore, if \( f \) has a left-inverse \( g_l \) and right-inverse \( g_r \), then these inverses must be the same function! This can be shown by considering:

[\[g_l = \quad ? \quad = g_l (f g_r ) = (g_l f) g_r = \quad ? \quad = g_r \]]

TODO: add diagram