Category Theory. Essence of associative composition.
Morphisms of a category obey the following two properties:
- Composition
- For any objects \( A, B, C \in \catobj{C} \), there is a function \( \cathom{C}(A, B) \times \cathom{C}(B, C) \to \cathom{C}(A, C) \).
- Associativity
- The idea of composition means that For any morphisms \( f, g, h \), \( h(gf) = (hg) f \).
Composition and the question of a category's datum
Are functions between sets of morphisms part of the datum of a category? Or are the sets of morphisms sufficient themselves, and there is simply a requirement that a function between the sets must be possible?
I'm not sure whether \( z \) is part of the datum of a category. A second phrasing of the composition property suggests that the functions are a datum of a category:
For any two morphisms \( f \in \cathom{C}(A, B) \) and \( g \in \cathom{C}(B, C) \) of category \( \cat{C} \) there is a morphism \( h \in \cathom{C}(A, C) \). Write \( gf \) as notation to represent \( h \).
The notation \( gf \in \cathom{C}(A, C) \) to represent the composition of \( f \) and \( g \) picks out a specific element of \( \cathom{C}(A, C) \), but this would not be possible if there isn't a specific function decided (maybe there are many possible functions).
Which of the two formulations is the true formulation is not just a question of conceptual framing. If the function \( z = \cathom{C}(A, B) \times \cathom{C}(B, C) \to \cathom{C}(A, C) \) is part of the datum of a category, then two categories could be considered different by having different compositional mapping \( z \) and \( z' \), both of the form \( \cathom{C}(A, B) \times \cathom{C}(B, C) \to \cathom{C}(A, C) \), while having the same sets of morphisms.
Directed graphs as a model of a category
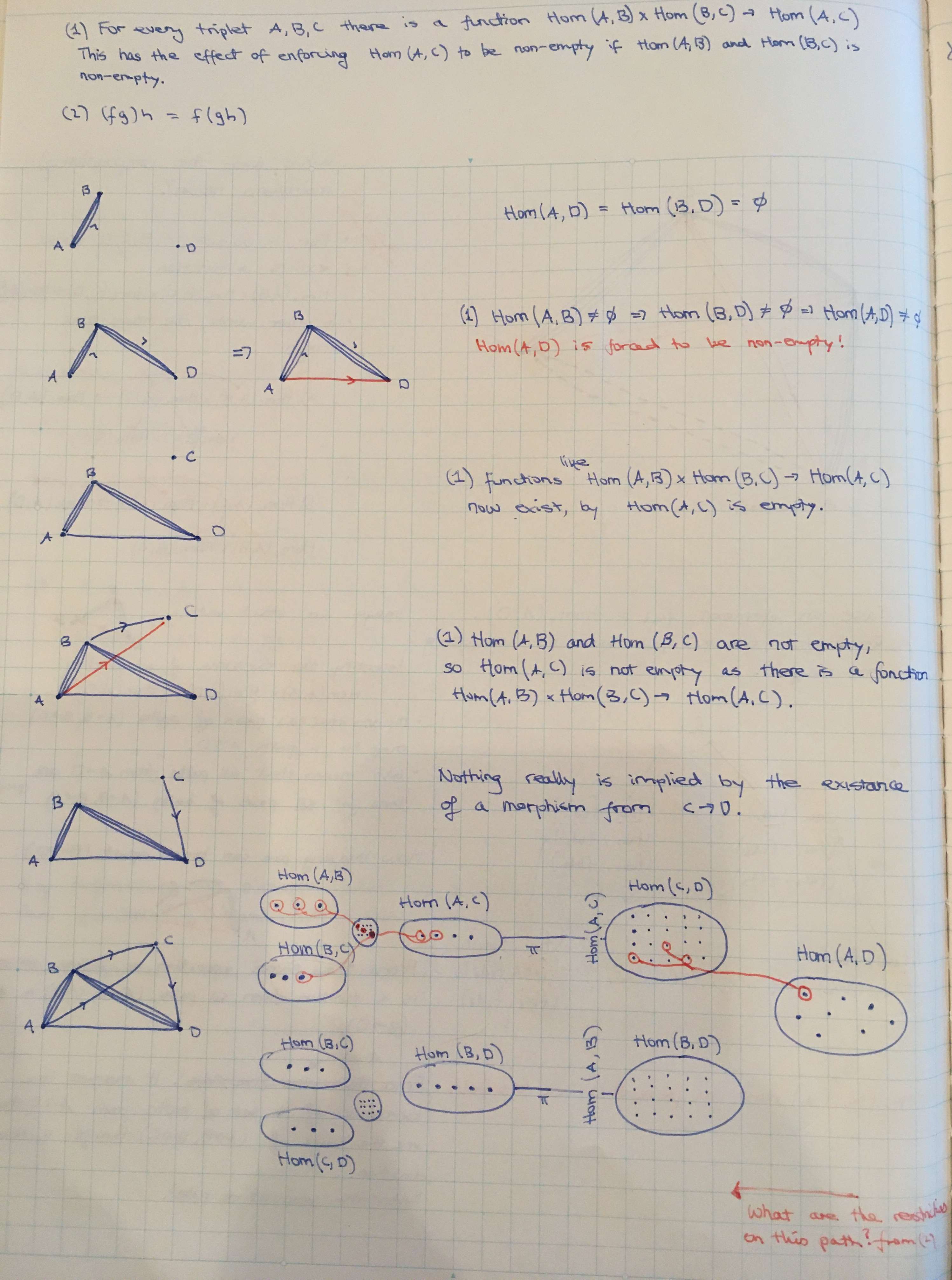
A directed graph is the best visual model I have found so far to represent the two above properties of morphisms. Nodes represent objects and edges represent morphisms. Composition and composition associativity place two restrictions on what graphs represent valid categories.
Composition
The composition property applied to a directed graph asserts that every pair \( (f, g) \in \cathom{C}(A, B) \times \cathom{C}(B, C) \) of directed edges that form a 2-edge path from \( A \) to \( C \) via \( B \) must correspond to a 1-edge path from \( A \) to \( C \). Thus, the former pair asserts the existance of the latter, and there is a function (possibly part of the category datum) that describes this mapping.
Associativity
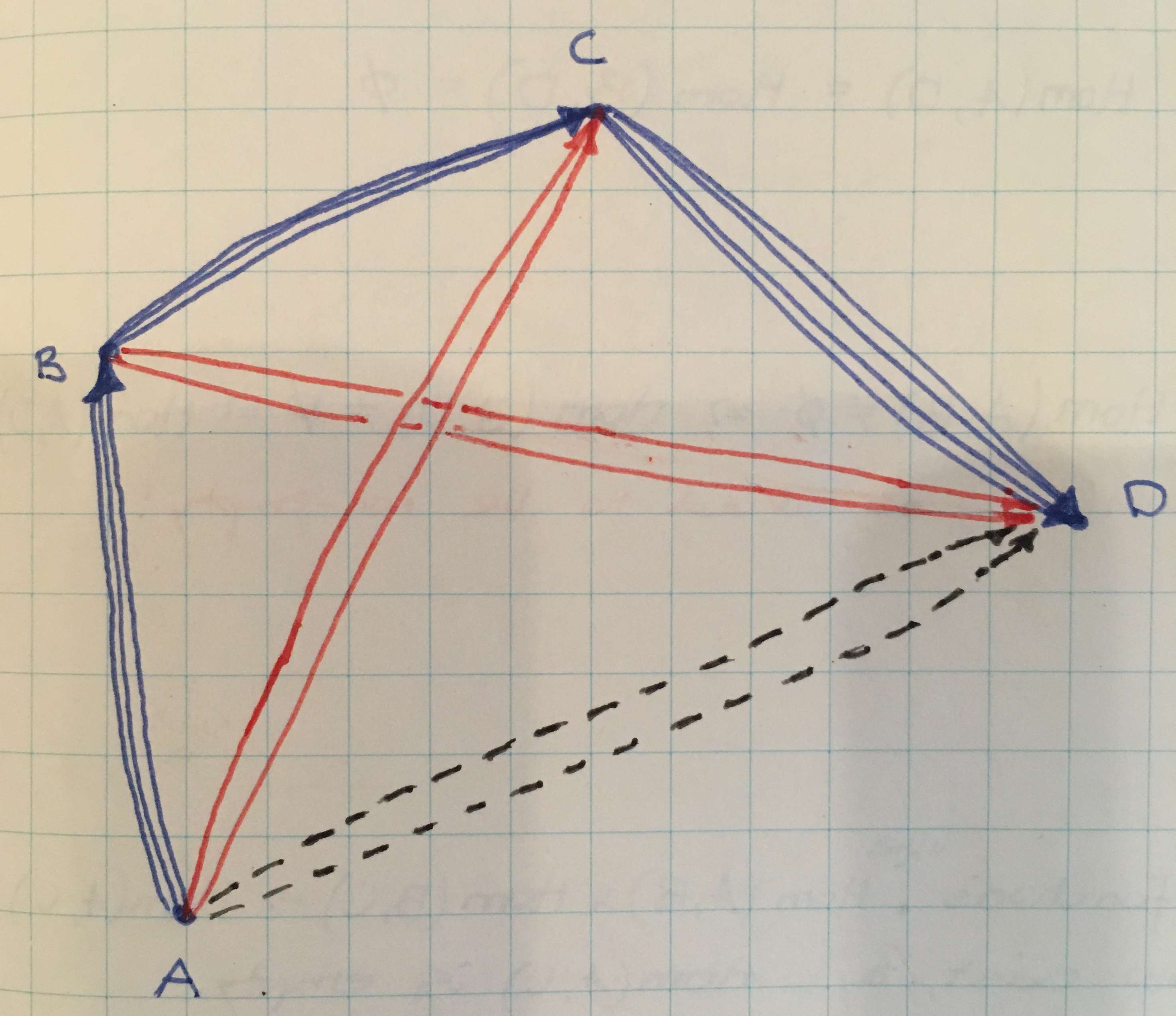
A 4 node graph is required to demonstrate the associativity of composition. In the graph below, there are many edges (morphisms) between the nodes. Pick out four edges \( f_{ab}, f_{bc}, f_{cd} \) and \( f_{ad} \). The naming indicates which set of morphim they belong to, for example, \( f_{ab} \in \cathom{C}(A, B)\).
To demonstrate associativity of composition, first we introduce two 2-edge paths: \( A \to B \to C \) and \( B \to C \to D \). Each 2-edge path represents a pair in a product space such as \( \cathom{C}(A, B) \times \cathom{C}(B, C) \). By composition of morphisms, each of these 2-edge paths have a correspondence with a 1-edge path; one is from \( A \) to \( C \) and one from \( B \) to \( D \).
2-edge path, \( A \to B \to C \)
The morphism pair \( (f_{ab}, f_{bc}) \) must map to a morphism in \( \cathom{C}(A, C) \), which we will denote as \( f_{ac} \). This mapping is done through a function \( z_1 : \cathom{C}(A, B) \times \cathom{C}(B, C) \to \cathom{C}(A, C) \). The preimage \( z_1^{-1}(f_{ac}) \) might contain many pairs of edges from \( A \to B \) and \( B \to C \), or it could contain just the pair \( (f_{ab}, f_{bc}) \).2-edge path, \( B \to C \to D \)
In a similar way, let \( f_{bd} \) be the morphism in \( \cathom{C}(B, D) \) which is the image of the morphism pair \( (f_{bc}, f_{cd}) \) through the function \( z_2 : \cathom{C}(B, C) \times \cathom{C}(C, D) \to \cathom{D}(B, D) \).
Associativity. Essence.
It is not possible for two different compound paths between the same nodes to have exactly the same 1-edge 'building blocks'. This is a phrase that tries to express the nature of composition associativity in a manner that appeals to intuition. A more concrete description follows.
Let \( z_3 : \cathom{C}(A, B) \times \cathom{C}(B, D) \to \cathom{C}(A, D) \) and \( z_4 : \cathom{C}(A, C) \times \cathom{C}(C, D) \to \cathom{C}(A, D) \) be mappings between sets of morphisms. These represent the correspondence from (the two sets of paths from \(A \to D \) which include one of the red edges) to (the set of 1-edge paths from \(A \to D \)). If \( g_1 = z_3((f_{ab}, f_{bd})) \) and \( g_2 = z_4((f_{ac}, f_{cd})) \), then associativity of composition asserts that \( g_1 = g_2 \). In otherwords, the 2-edge path from \( A \) to \( D \) via \( B \) and the 2-edge path from \( A \) to \( D \) via \( C \) must map to the same 1-edge path from \( A \) to \( D \). This is so as both of these paths have a preimage through \( z_1 \) and \( z_2 \) respectively which 'unfold' as the same ordered 3-tuple \( (f_{ab}, f_{bc}, f_{cd}) \).
The word 'unfold' in the previous sentence does a lot of heavy lifting. The edge \( g = g_1 = g_2 \) might be one of many edge in \( \cathom{C}(A, D) \). However, if, following \( g \) recursively back through preimages 'touch' a path tuple, such as \( (f_{ab}, f_{bc}, f_{cd}) \), then no other edge in \( \cathom{C}(A, D) \) can 'touch' this tuple, no matter how the morphism mappings are recursively passed through.