Slice category
A slice category is an example of a category whose objects are [something] and whose morphisms are also [one of those something].
The objects of a slice category are ambient morphisms [to or from?] an object in an ambient category, and the morphisms of a slice category are ambient morphisms from one slice category object to another. The precise definition is as follows:
Slice category
Let \( \cat{C} \) be a category and let \( A \) be an object of \( \cat{C} \). Then we define \( \cat{C_A} \) to be the category whose objects and morphisms are as follows:
- \( \catobj{C_A} = \) the set of all morphisms from any object in \( \cat{C} \) to the object \( A \). Thus, [\( f \in \catobj{C_A} \iff \; ? \; \text{ for some object } Z \in \catobj{C} \)].
- For any two objects \( f_1: Z_1 \to A \) and \( f_2: Z_2 \to A \) in \( \cat{C_A} \), \( \cathom{C_A}(f_1, f_2) \) contains any morphism [\( \sigma \in \; ? \)] such that [\( ? = \; ? \) ].
Here is diagram representing two objects \( f_1 \) and \( f_2 \) of \( \cat{C_A} \).
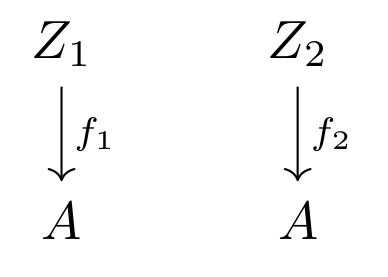
Here is a diagram of the same two objects including a morphism in \( \cathom{C_A}(f_1, f_2) \). The morphism \( \sigma \) of \( \cat{C_A} \) is a morphims of \( \cat{C} \) such that \( f_1 = f_2 \sigma \).
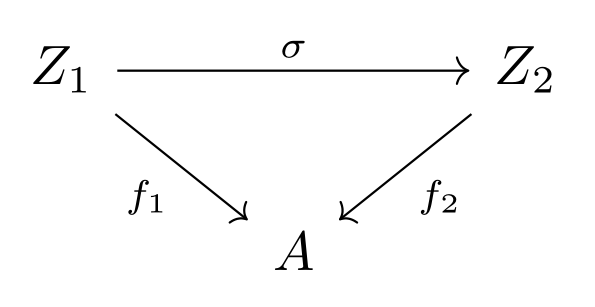
Aluffi describes the morphisms of \( \cat{C_A} \) as being commutative diagrams in the ambient cantegory, where ambient category refers to \( \cat{C} \).
It is worthwhile checking that the category \( \cat{C_A} \) as described is indeed a valid category, according to the definition of a category.
