\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
Math and science::Algebra::Aluffi

Slice category

A slice category is an example of a category whose objects are morphisms of some other category and whose morphisms are also morphism of that original category. 

The objects of a slice category are ambient morphisms to an object in an ambient category, and the morphisms of a slice category are ambient morphisms from one slice category object to another. The precise definition is as follows:

Slice category

Let \( \cat{C} \) be a category and let \( A \) be an object of \( \cat{C} \). Then we define \( \cat{C_A} \) to be the category whose objects and morphisms are as follows:

  • \( \catobj{C_A} = \) the set of all morphisms from any object in \( \cat{C} \) tothe object \( A \). Thus, \( f \in \catobj{C_A} \iff f \in \cathom{C}(Z, A) \text{ for some object } Z \in \catobj{C}\).
  • For any two objects \( f_1: Z_1 \to A \) and \( f_2: Z_2 \to A \) in \( \cat{C_A} \), \( \cathom{C_A}(f_1, f_2) \) contains any morphism \( \sigma \in \cathom{C}(Z_1, Z_2) \) such that \( f_2 \sigma = f_1 \).

The back side has an diagram of a slice category. Can you remember what it looks like? There is also info on co-slice categories. Can you remember the definition?


Here is diagram representing two objects \( f_1 \) and \( f_2 \) of \( \cat{C_A} \).

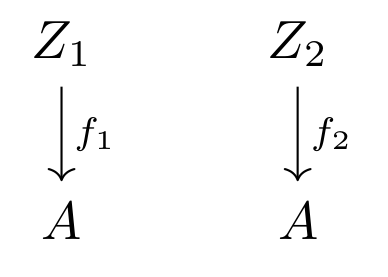
Here is a diagram of the same two objects including a morphism in \( \cathom{C_A}(f_1, f_2) \). The morphism \( \sigma \) of \( \cat{C_A} \) is a morphims of \( \cat{C} \) such that \( f_1 = f_2 \sigma \).

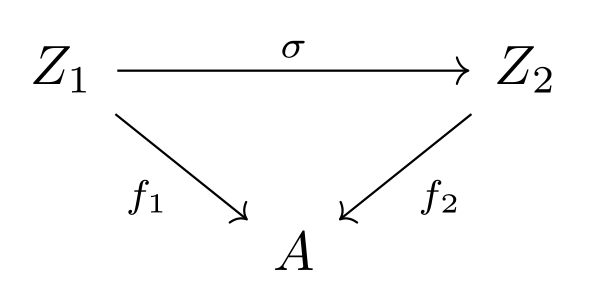
Aluffi describes the morphisms of \( \cat{C_A} \) as being commutative diagrams in the ambient cantegory, where ambient category refers to \( \cat{C} \).

It is worthwhile checking that the category \( \cat{C_A} \) as described is indeed a valid category, according to the definition of a category.

Coslice category

Coslice categories are similar to slice categories, and we make use of this similarity to give a compressed definition below.

Let \( \cat{C} \) be a category and \( A \) be an object of \( \cat{C} \). A coslice category \( \cat{C_A} \) is one whose objects which are morphisms in \( \cat{C} \) from the object \( A \) to another object in \( \cat{C} \). The morphisms of \( \cat{C_A} \) are the morphims of \( \cat{C} \) such that they form commutative diagrams with two objects in \( \cat{C_A} \).

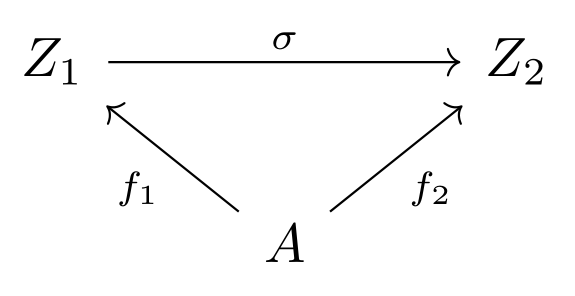
Here is a diagram representing two objects, \( f_1 \) and \( f_2 \), and a morphism \( \sigma \) of a coslice category where \( A \) is an object of the ambient category.

Example

Slice category example

Let \( \cat{C} \) be the category determined by a relation \( R \) on the set of integers:

  • \( \catobj{C} = \mathbb{Z} \);
  • for any objects \( a, b \in \mathbb{Z} \), \( \cathom{C}(a, b) = \{ (a, b) \} \text{ if } aRb, \text{ else } \{ \} \) (the entry in the graph representation of the \( \le \) relation at row \( a \) and column \( b \)).

Then let \( \cat{C_3} \) be the slice category where the objects are the morphisms of \( \cat{C} \) whose target is \( 3 \). \( (0, 3), (-4, 3), (2, 3), \) and \( (3, 3) \) are examples of objects of \( \cat{C_3} \). For objects \( (n, 3) \) and \( (m, 3) \) in \( \cat{C_A} \) (where \( n, m \le 3 \)), there is one morphism from \( (n, 3) \) to \( (m, 3) \) as long as \( n \le m \); that morphism will be \( (n, m) \), which also exists in category \( \cat{C} \) from \( n \to m \).

Aluffi mentions that the category \( \cat{C_3} \) can be "harmlessly identified" with the 'subcategory' of integers \( \le 3 \)."

Coslice category example

Define a category, denoted as \( \mathrm{Set}^* \), to be a coslice category where the ambient category is the category of sets-functions, \( \mathrm{Set} \), and the target, \( A \in \catobj{\mathrm{Set}} \), is some singleton set, denoted as \( \{*\} \).

  • An object of \( \mathrm{Set}^* \) is a function \( f : \{ * \} \to S \), for some set \( S \). The datum of such an object is both the choice of a non-empty set \( S \) and a single element within \( S \) what is mapped to the single element of the singleton set. Thus, objects of \( \mathrm{Set}^* \) can be denoted as set-element pairs, \( (S, s) \), where \( S \) is a set and \( s \in S\). Such pairs are called pointed sets.
  • A morphism of \( \mathrm{Set}^* \), between two objects \( (S, s ) \) and \( (T, t) \) is any function \( \sigma : S \to T \) with the requirement that \( \sigma \) sends \( s \) to \( t \). So, if both \( S \) and \( T \) and not singletons, then, then there will be multiple morphisms between \( (S, s) \) and \( (T, t) \).