\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
Math and science::Algebra::Aluffi

Isomorphism

For functions between sets, we defined the notion of injective, surjective and bijective/isomorphic functions. We do the same for morphisms between objects of a category. This card covers isomorphisms; other cards cover monomorphisms and epimorphisms.

An isomorphism is defined as follows:

Isomorphism. Definition.

Let \( C \) be a category. A morphism \( f \in \cathom{C}(A, B) \) is an isomorphism iff there exists a morphism \( g \in \cathom{C}(B, A) \) such that both:

\[ gf = 1_A, \quad fg = 1_B. \]

\( g \) is said to be a (two sided) inverse of \( f \).

Uniqueness

Can \( f \) have multiple inverses? Uniqueness of \( g \) is not built into the definition above; however, it is indeed true that \( g \) is unique:

Theorem

An inverse of an isomorphism is unique.

Proof on the other side.

Since an inverse is unique, there is no ambiguity in denoting it as \( f^{-1} \).

Auxiliary propositions

Here are three useful propositions related to isomorphisms:

  • Every identity is an isomorphism and is its own inverse.
  • If \( f \) is an isomorphism then \( f^{-1} \) is an isomorphism and \( (f^{-1})^{-1} = f \).
  • If \( f \in \cathom{C}(A, B) \) and \( g \in \cathom{C}(B, C) \) are isomorphisms, then \( g\, f \) is an isomorphism and \( (g \, f)^{-1} = f^{-1}g^{-1} \).

An inverse of an isomorphism is unique. Proof.

Let \( f : A \to B \) be a morphism, let \( g_1 : B \to A \) be a left-inverse of \( f \) and let \( g_2 : B \to A \) be a right-inverse of \( f \). Thus,

\[ g_1 \,f = 1_A, \quad f \, g_2 = 1_B \]

By composing \( g_1 \), \( f \) and \( g_2 \) then applying associativity we see that \( g_1 = g_2 \) and that this morphism is the unique inverse:

\[ g_1  (f \, g_2) = g_1 \, 1_B = g_1, \quad (g_1 \, f)  g_2 = 1_A \, g_2 = g_2 \]

The fact that \( g_1 ( f \, g_2) = (g_1 \, f) g_2 \) is asserted by the definition of categories. Applying this we arrive at \( g_1  = g_2 \). 

Intuition

The diagram below might spark some intuition. The composition of \( g_1 \), \( f \) and \( g_2 \) is presented in the two possible: the left side constructs the path beginning with \( g_2 \) and the right side beginning with \( g_1 \).

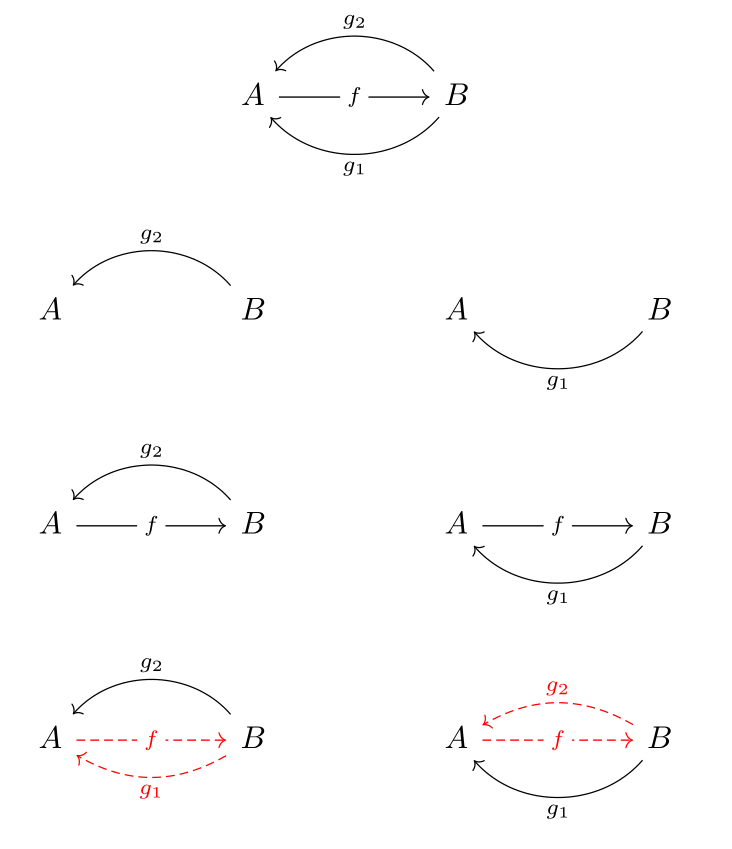
One intuitively appealing description of the diagram is that there is a three step journey where the middle leg, \( f \), can negate either the first leg, \( g_2 \), or the last leg \( g_1 \). Regardless of which one is negated, the overall journey is the same (associativity). If \( g_1 \) is negated, then the journey is \( g_2 \), and if \( g_2 \) is negated the journey is \( g_1 \), but either way, the journel is the same, so \( g_1 = g_2 \).

Departure from \( \mathrm{Set} \) 

While many aspects of functions on sets transfer nicely to the catagorical setting, it is noteworthy that a morphism that is monomorphic and epimorphic (concepts which are analogous to injectivity and surjectivity of functions) may not necessarily be isomorphic. In comparison, a function is both injective and surjective iff it is bijective.

Source

p28