\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
Math and science::Analysis::Tao::06. Limits of sequences

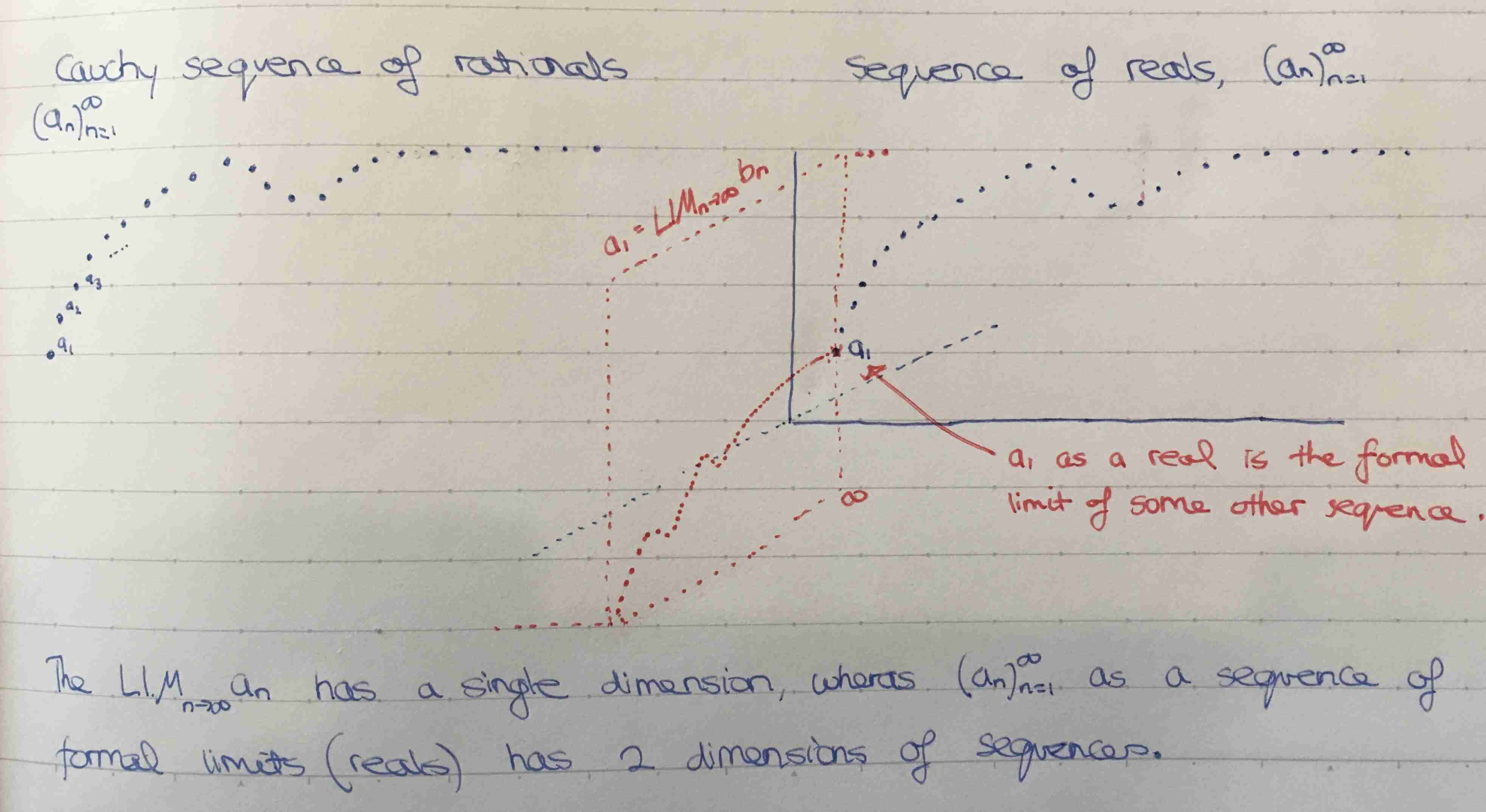
Formal limits are genuine limits

Suppose that \( (a_n)_{n=1}^{\infty} \) is a Cauchy sequence of rational numbers (defined for reals). Then \( (a_n)_{n=1}^{\infty} \) converges to \( LIM_{n\to\infty}a_n \), i.e.


\[ \lim_{n\to\infty}a_n = LIM_{n\to\infty}a_n \]


The real defined by the Cauchy sequence is equal to the real to which the matching sequence of reals converges to.

Going forward, this equality allows limits to be used inplace of formal limits. Underneath, however, each real is still defined as a formal limit of rationals.

This masking of the foundations was similarly undertaken for rationals, integers and natural numbers. The pair of integers combined with '//' to make a rational, the pair of natural numbers combined with '—' to make an integer, and the increment operation—all were masked by subsequently defined operations.

Context

Cauchy sequences of reals → convergence of sequences of reals → uniqueness of convergence→ limit, the definition → subsumption of formal limits

Source

Tao, Analysis I
Chapter 6