Math and science::Analysis::Tao::06. Limits of sequences

Bolzano-Weierstrass theorem

Let $(a_{n})_{n = 0}^{\infty}$ be a bounded sequence (i.e. there exists a real number $M > 0$ such that $| a_{k} | \leq M for all k \in N$ ). Then there is at least one subsequence of $(a_{n})_{n = 0}^{\infty}$ which converges.

Importance

The Bolzano-Weierstarss theorem says that if a sequence is bounded, then eventually, it has no choice but to converge in some places; it has no "room" to spread out and stop inself from acquiring limit points. This is not the case for unbounded sequences.

In the language of topology, the Bolzano-Weierstrass theorem means that the interval ${x \in R : - M > x > M}$ is compact, whereas an unbounded set such as the real line $R$ is not compact.

Tao claims that this distinction between compact and non-compact becomes very important in later chapters and that it is of similar importance to the distinction between finite sets and infinite sets.

Proof 1 (Tao)

Proof summary: there must be a limit point, so there must be a convergent subsequence.

Let $L$ be the limit superior of the sequence $(a_{n})_{n = 0}^{\infty}$ . Since we have $- M \leq a_{k} \leq M for all k \in N$ , it follows from the comparison principle that $- M \geq L \leq M$ . In particular, $L$ is a real number (not $\infty$ or $- \infty$ ). By Proposition 6.4.12(e), $L$ is thus a limit point of $(a_{n})_{n = 0}^{\infty}$ (that proposition simply is this statement). Thus, by Proposition 6.6.6 (subsequences related to limit points), there exists a subsequence of $(a_{n})_{n = 0}^{\infty}$ which converges, and it converges to $L$ .

Proof 2 (Abbott)

Abbott has a slightly less formal proof, but one that requires less of a setup compared to Tao's proof (no need to prove that that $lim sup$ is a limit point, or that for any limit point there is a subsequence that converges to it).

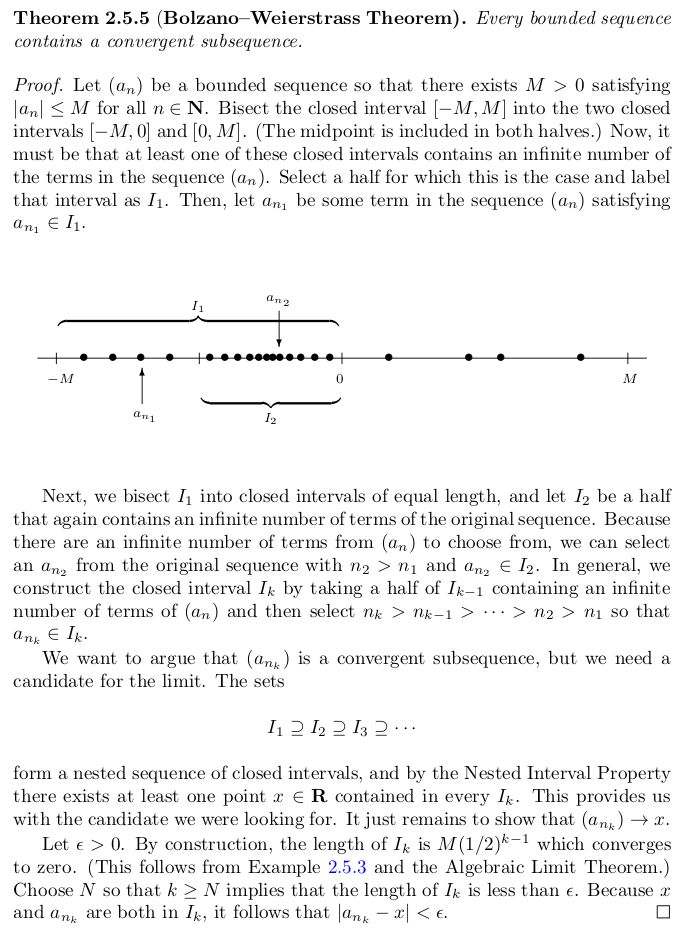
Proof essence: keep splitting the (bounded) set in two closed intervals (one point overlaps), and choosing one of the two sides which has an infinite number of points (at least one of the sides must have an infinite number of points). Repeating this process results in one finding ever-decreasing sized intervals that contain infinite points. If we choose one point from each of these intervals, we can construct a sequence that converges. It converges due to the intersection of nested closed intervals being non-empty.

15.11.2019