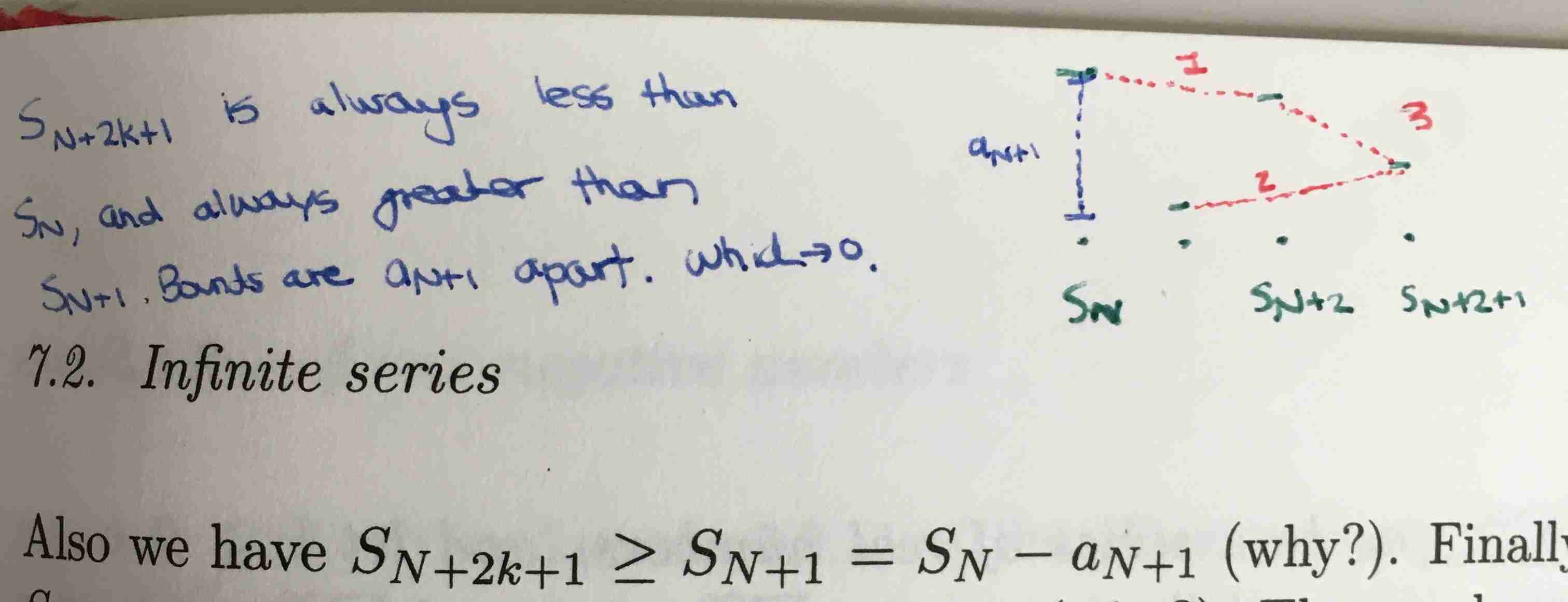Math and science::Analysis::Tao::07. Series

Alternating series test

An alternating series converges if the sequence of elements converges absolutely to zero.

Let $(a_{n})_{n = m}^{\infty}$ be a sequence of real numbers which are non-negative and decreasing, thus $a_{n} \geq 0$ and $a_{n} \geq a_{n + 1}$ for every $n \geq m$ . Then the series $\sum_{n = m}^{\infty} (- 1)^{n} a_{n}$ is convergent if and only if the sequence $(a_{n})_{n = m}^{\infty}$ converges to 0 as $n \to \infty$ .

There is some weight to this proposition, as non-alternating series do not have this property. For example, the series $\sum_{n = m}^{\infty} \frac{1}{n}$ does not converge. But, $\sum_{n = m}^{\infty} (- 1)^{n} \frac{1}{n}$ in comparison will converge to zero.

Proof outline

The below approach is summarized as:

Let $N$ be even. For any $k > 0$ , $S_{N + k}$ is less than $S_{N}$ but greater than $S_{N + 1}$ . The difference between $S_{N}$ and $S_{N + 1}$ approaches zero because the sequence $(a_{n})_{n = m}^{\infty}$ approaches zero. So the sequence of sums $(S_{n})_{n = m}^{\infty}$ is $ε$ -steady for every $ε > 0$ .

Proof

This proof is crafty, and my attempts at an alternative failed, so there is some value in internalizing the approach.

One side of the iff relationship is easy. From the zero test for series, we know that if $\sum_{n = m}^{\infty} (- 1)^{n} a_{n}$ is a convergent series, then the sequence $((- 1)^{n} a_{n})_{n = m}^{\infty}$ converges to 0, and by the zero test for sequences, we can infer that the sequence ( $a_{n})_{n = m}^{\infty}$ must also converge to zero.

Now suppose conversly that ( $(- 1)^{n} a_{n})_{n = m}^{\infty}$ converges to 0. For each $N \geq m$ , let $S_{N}$ be the partial sum $S_{N} := \sum_{n = m}^{N} (- 1) a_{n}$ ; our job is to show that $(S_{N})_{N = m}^{\infty}$ converges. Observe that

\begin{aligned} S_{N + 2} & = S_{N} + (- 1)^{N + 1} a_{N + 1} + (- 1)^{N + 2} a_{N + 2} \\ = S_{N} + (- 1)^{N + 1} (a_{N + 1} - a_{N + 2}) \end{aligned}

By hypothesis $(a_{N + 1} - a_{N + 2})$ is non-negative. Thus we have $S_{N + 2} \geq S_{N}$ , when $N$ is odd and $S_{N + 2} \leq S_{N}$ when $N$ is even. Now suppose that $N$ is even. [What is nice is the the proof proceeds without needing to consider the other case. We arrive at an inequality that works for what we need.]

From the above discussion and induction we see that both:

$S_{N + 2 k} \leq S_{N}$ and $S_{N + 2 k + 1} \geq S_{N + 1} = S_{N} - a_{N + 1}$ for all natural numbers $k$ . Also we have $S_{N + 2 k + 1} = S_{N + 2 k} - a_{N + 2 k + 1} \leq S_{N + 2 k}$ . Combining all of this we can say:

S_{N} - a_{N + 1} \leq S_{N + 2 k + 1} \leq S_{N + 2 k} \leq S_{N} for all k

This means that

S_{N} - a_{N + 1} \leq S_{n} \leq S_{N} for all n \geq N

This is enough for us to be able to say that $(S_{n})_{n = m}^{\infty}$ is eventually $a_{N + 1}$ -steady. But the sequence $(a_{N})_{N = m}^{\infty}$ converges to 0 as $N \to \infty$ , which implies that $(S_{n})_{n = m}^{\infty}$ is eventually ε-steady for every $ε > 0$ . Thus, $(S_{n})_{n = m}^{\infty}$ converges, and so the series $\sum_{n = m}^{\infty} (- 1)^{n} a_{n}$ is convergent.

21.11.2019