\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
Math and science::Analysis::Tao::07. Series

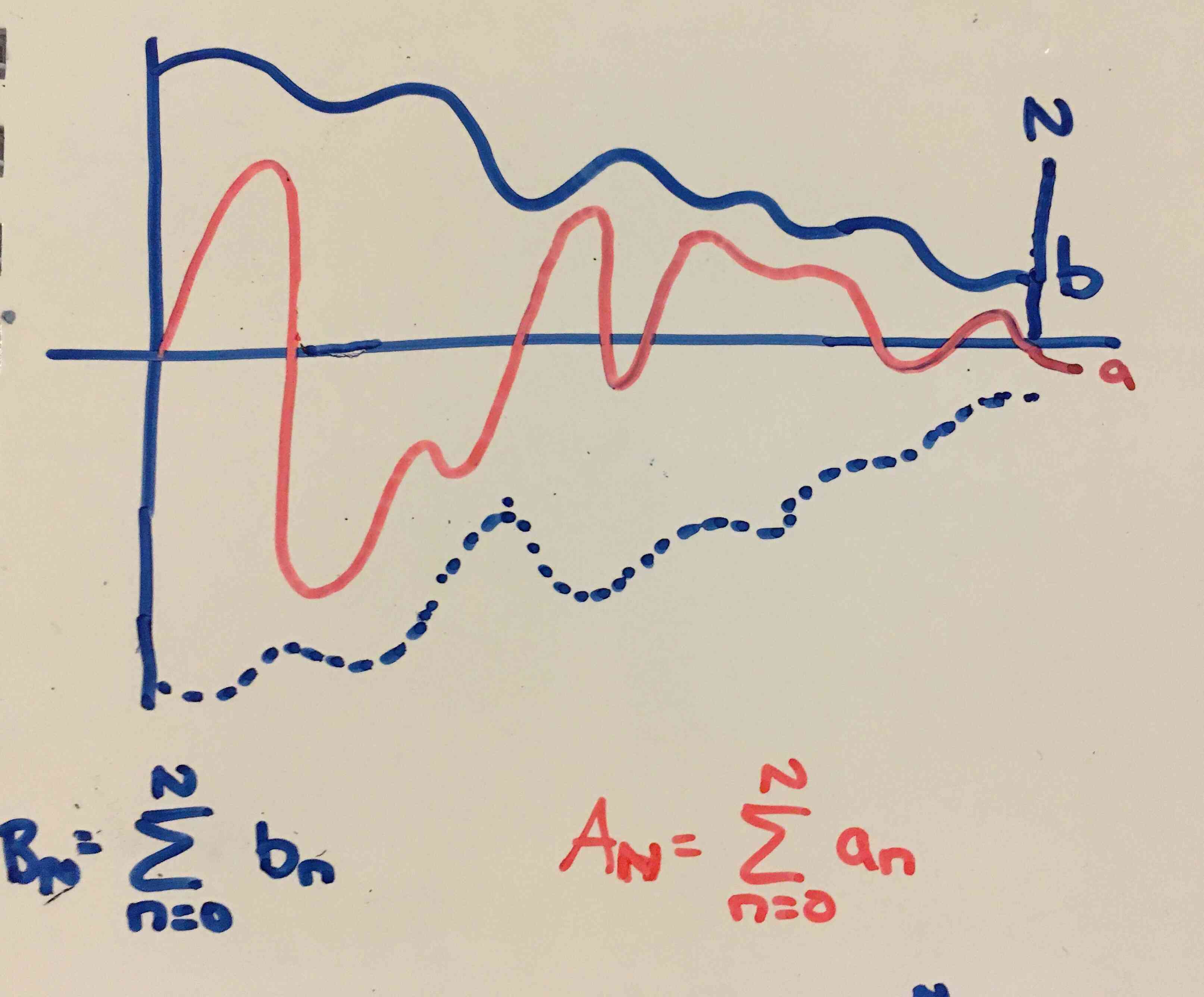
The comparison test (and bounded series of non-negative numbers)

We wish to extend the comparison test for finite series to apply to infinite series.

For finite series, the comparison test appeared as a simple opening lemma (7.1.4 f):

\[ \text{When } a_i \le b_i \text{ we have } \sum_{i=m}^{n} a_i \le \sum_{i=m}^{n} b_i \]

For infinite series, we can only make this statement when \( |a_i| \le b_n \), otherwise the sum for \( a \) could diverge. We set this up and prove it below.

First, a useful (and very simple) proposition.

Sums of non-negative numbers are bounded iff they are convergent.

Let \( \sum_{n=m}^{\infty}a_n \) be a formal series of non-negative real numbers. Then this series is convergent if and only if there is a real number \( M \) such that

\[ \sum_{n=m}^{N}a_n \le M \text{ for all integers } N \ge m \]

Proof

Two earlier propositions are:

  • Every convergent sequence of real numbers is bounded (6.1.17).
  • An increasing sequence which has an upper bound is convergent (6.3.8).

The sequence \( (S_N)_{n=m}^{\infty} \) representing the series \( \sum_{n=m}^{\infty}a_n \) is increasing, by definition. So the above two propositions form each side of the proposition's iff statement. 

Now we can introduce the comparison test.

Comparison test

Let \( \sum_{n=m}^{\infty}a_n \) and \( \sum_{n=m}^{\infty}b_n \) be two formal series of real numbers, and suppose that \( |a_n| \le b_n \) for all \( n \ge m \) (thus all numbers in \( (b_n) \) must be non-negative). Then if \( \sum_{n=m}^{\infty}b_n \) is convergent, then \( \sum_{n=m}^{\infty}a_n \) is absolutely convergent, and in fact

\[  \left| \sum_{n=m}^{\infty}a_n \right| \le \sum_{n=m}^{\infty}|a_n| \le  \sum_{n=m}^{\infty}b_n \]

Proof

Let \( SA_N := \sum_{n=m}^{N}|a_n|  \) be the Nth partial sum of \(  \sum_{n=m}^{\infty}|a_n| \) and \( SB_N := \sum_{n=m}^{N}b_n \) be the Nth partial sum of \( \sum_{n=m}^{\infty}b_n \). As \( \sum_{n=m}^{\infty}b_n \) is bounded according to the proposition above, and by the the comparison test for finite series we have: \[ SA_N \le SB_N \le M \text{ for all } N \ge m \text{ and for some bounding real } M \] Through this transitivity, \( (SA_N)_{N=n}^{\infty} \) also meets the conditions for being bounded. Then from the above propositive again, it must be that \( \sum_{n=m}^{\infty}|a_n| \) is convergent. The Absolute Convergence Test informs us that absolute convergence implies conditional convergence, and in addition that \( \left| \sum_{n=m}^{\infty}a_n \right| \le \sum_{n=m}^{\infty}|a_n| \). Thus, with all of the below infinite series converging we can compare them like so:
\[ \left| \sum_{n=m}^{\infty}a_n \right| \le \sum_{n=m}^{\infty}|a_n| \le \sum_{n=m}^{\infty}b_n \]

We can also run the Comparison Test in the contrapositive:

If \( \sum_{n=m}^{\infty}a_n \) is not absolutely convergent then \( \sum_{n=m}^{\infty}b_n \) is not conditionally convergent.


Source

p171