\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
Math and science::Analysis::Tao::08. Infinite sets

Countable sets

A set \( X \) is said to be countably infinite (or just countable) iff it has equal cardinality with with the natural numbers \( \mathbb{N} \). 

We also have the terms: at most countable and uncountable.

  • A set is at most countable if it is either finite or coutable.
  • A set is uncountable if it is infinite and not countable.
The relationship is shown below:



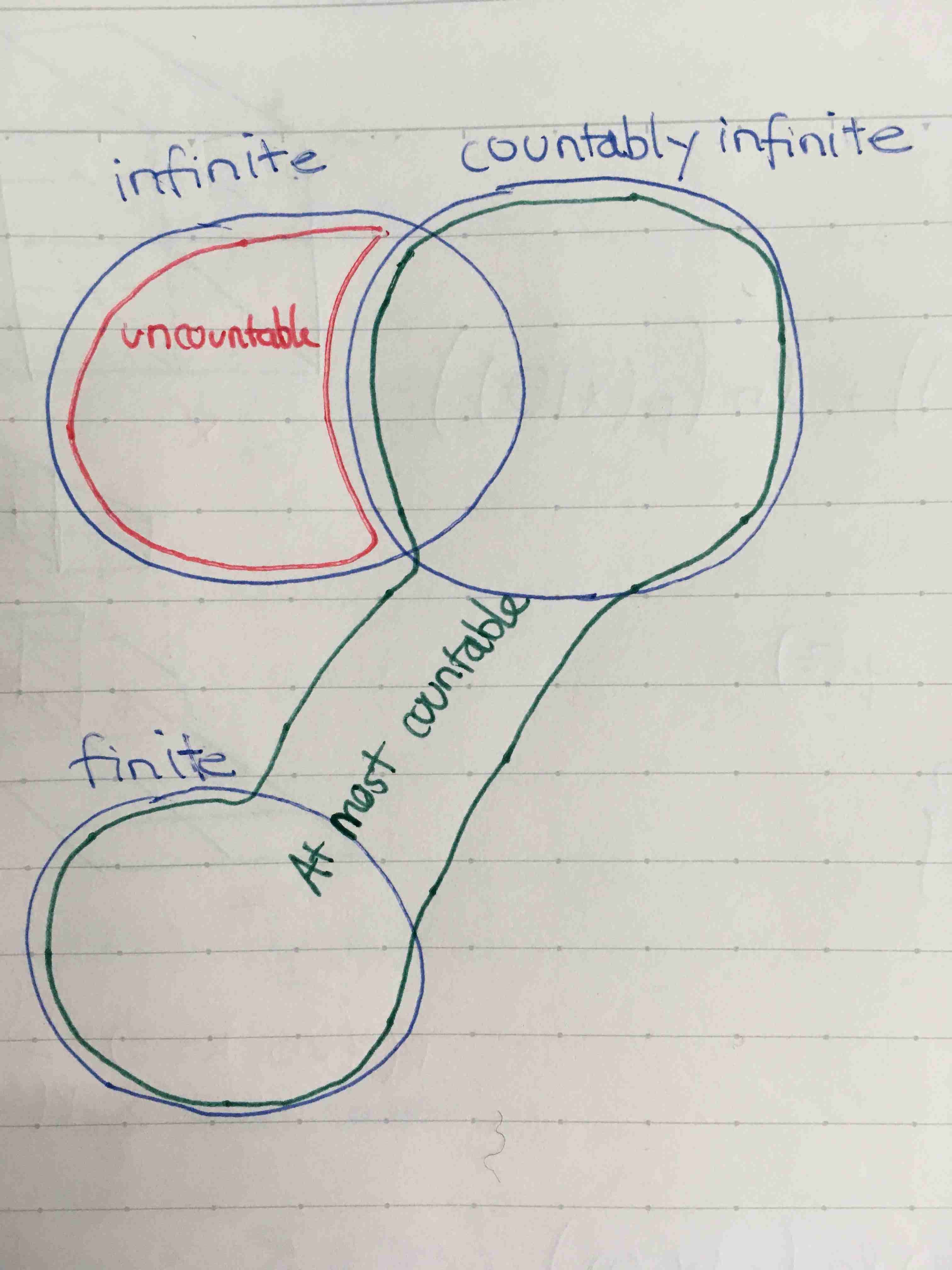
Countably infinite sets are also called denumerable sets.

Note that a countable set must be infinite as it has the same cardinality as \( \mathbb{N} \).

Know your bijection

To understand the nature of countable sets, it is crucial to understand the nature of the bijection and how it operates on the infinite set \( \mathbb{N} \). Recap below:

One-to-one functions

A function \( f \) is one-to-one (or injective) if different elements map to different elements:

\[ x \neq x' \implies f(x) \neq f(x') \]

Onto functions

A function \( f \), \( f : X \rightarrow Y \) is onto (or surjective) if every element in \( Y \) can be obtained from applying \( f \) to some element in \( X \):

\[ \text{For every } y \in Y \text{, there exists an } x \in X \text{ such that } f(x) = y \]

Bijective functions

A function which is both injective and surjective is called bijective or invertable.

Example

We know that if \( X \) is finite and \( Y \) is a propper subset of \( X \), then \( Y \) does not have the same cardinality as \( X \). This does not apply to infinite sets. For example, \( \mathbb{N} \) has the same cardinality as \( \mathbb{N} - \{0\} \), and thus, the latter is countable. This is so as we can have a bijection \( f: \mathbb{N} \rightarrow \mathbb{N} - \{x\} \) from \( \mathbb{N} \) to \( \mathbb{N} - \{x\} \). (why? Look at the bijective definition above)

The set of even natural numbers, \( \{2n : n \in \mathbb{N} \} \), is also countable.