\(
\newcommand{\cat}[1] {\mathrm{#1}}
\newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})}
\newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}}
\newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}}
\newcommand{\betaReduction}[0] {\rightarrow_{\beta}}
\newcommand{\betaEq}[0] {=_{\beta}}
\newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}}
\newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}}
\)
Math and science::Analysis::Tao::08. Infinite sets
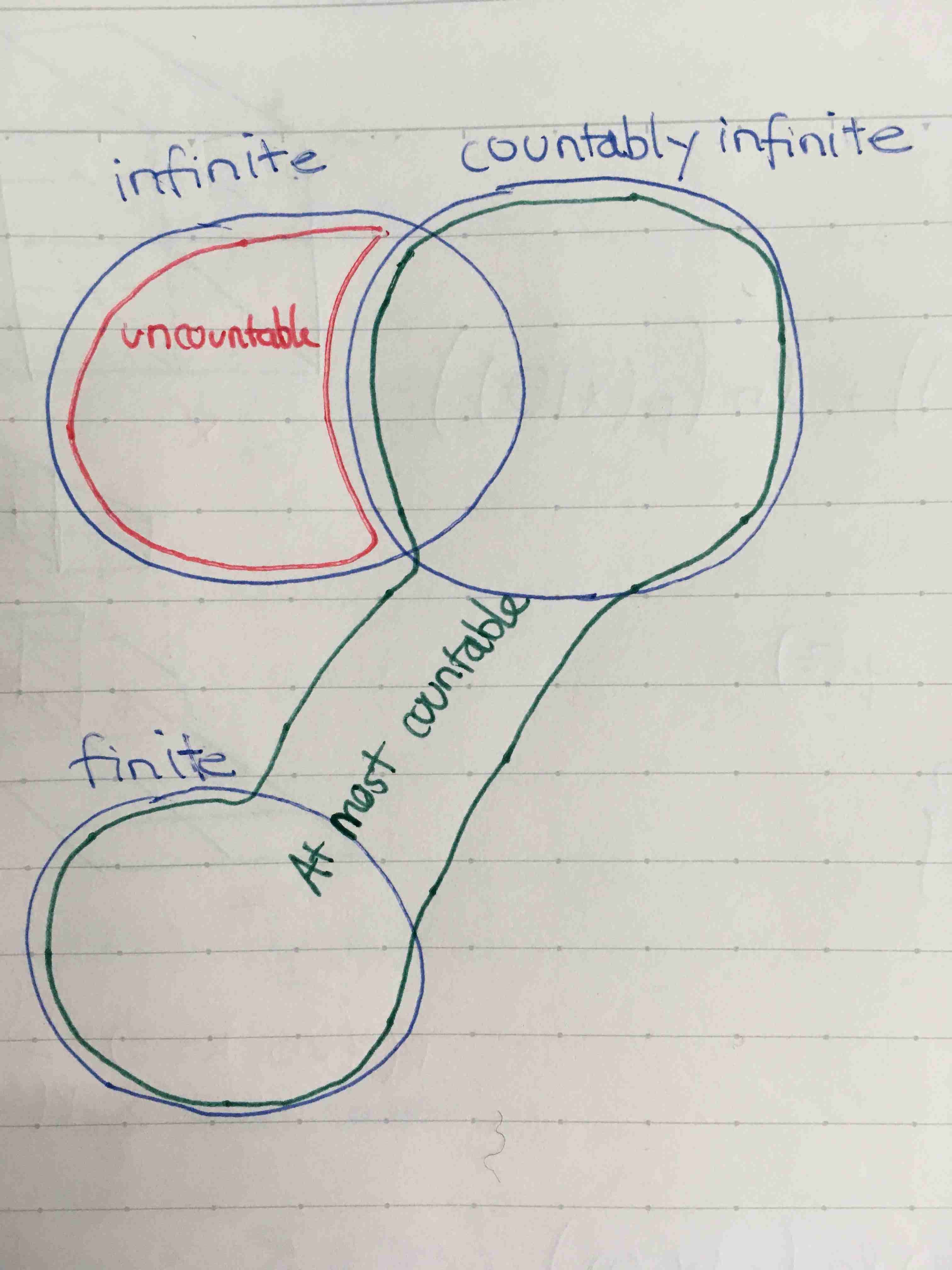
Countable sets
A set \( X \) is said to be countably infinite (or just countable)
iff [...].
We also have the terms: at most countable and uncountable.
- A set is at most countable if it is [...].
- A set is uncountable if it is [...].
The relationship is shown below: