\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
Math and science::Analysis::Tao, measure::02. Lebesgue measure

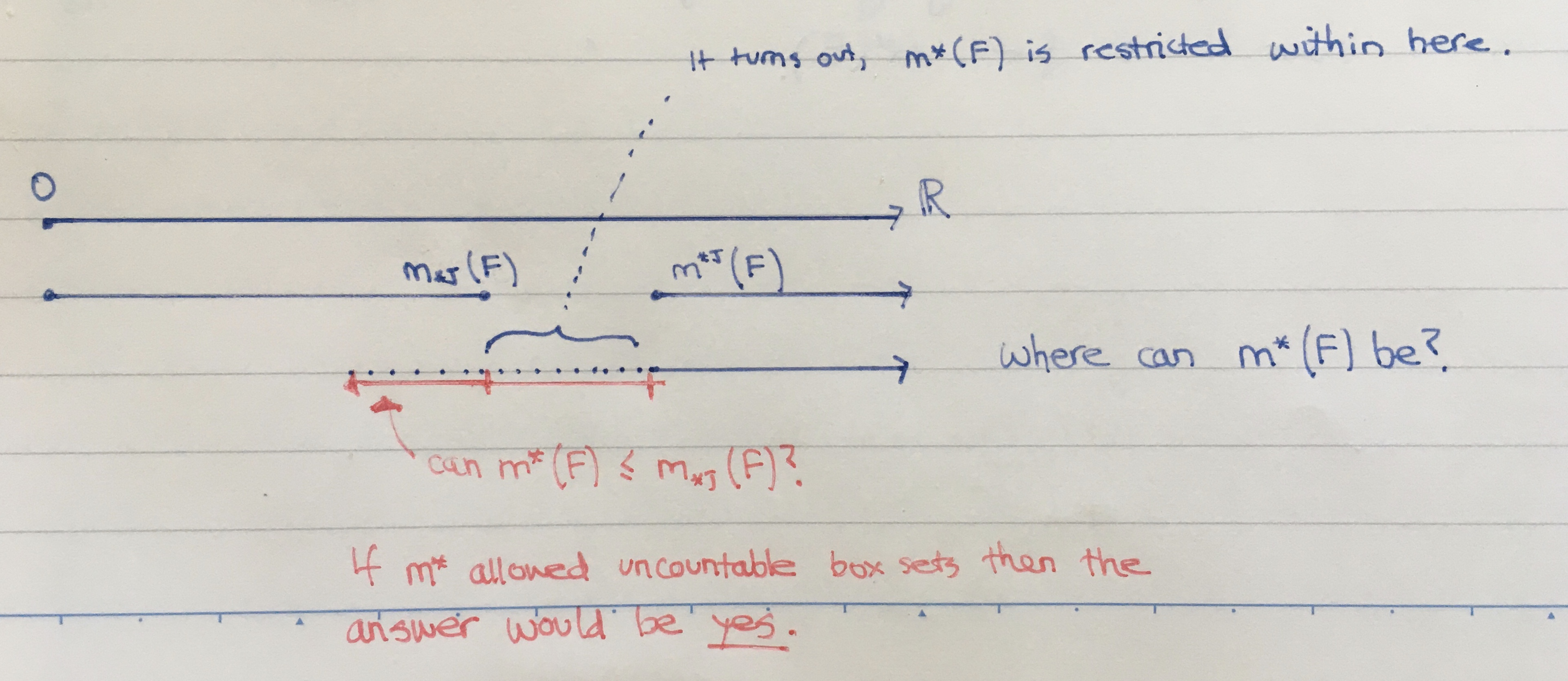
Lebesgue outer measure is between the Jordan inner and outer measures

This relation is useful to ground one's mental model of Lebesgue measure.

\[ m_{*,(J)}(F) \le m^*(F) \le m^{*,(J)}(F) \]

The proof outline for the rightmost inequality is simple. The leftmost inequality is not simple, it is somewhat profound.

1. Rightmost inequality, proof outline

\[ m^*(F) \le m^{*,(J)}(F) \]

In words: the Lebesgue outer measure is less-equal to the the Jordan outer measure.

Consider the set of all at-most-countable box covers for the set \( F \subset \mathbb{R}^d \); denote it by \( \mathcal{S} \). The real \( m^*(F) \) is the greatest lower bound for the volume of these covers. Contained as a subset off these covers is the set of all finite box covers; denote it as \( \mathcal{C} \). \( m^*(F) \) is a lower bound (the greatest) for \( \mathcal{S} \), so it must also be a lower bound for the subset \( \mathcal{C} \). The real \( m^{*,(J)}(F) \) is the greatest lower bound for \( \mathcal{C} \), so we have \( m^*(F) \le m^{*,(J)(F) } \).

2. Leftmost inequality. It's not trivial.

\[ m_{*,(J)}(F) \le m^*(F) \]

In words: the Lebesgue outer measure is not less than the Jordan inner measure.

The same logic as above seems to intuitively fit, but it doesn't.

Not a Lebesgue inner measure

Any finite set of boxes contained in \( F \) is not in the set of countable covers of \( F \). We are not comparing the Jordan inner measure \( m_{*,(J)}(F) \) to some countable extension. Such a real would be a supremum (not an infimum like the outer measure) and might look like:

\[ m_{*}(F) := \sup \left( \{ m \in \mathbb{R} : m = \sum_{b \in I} |b| \text{, for some countable collection of boxes, } I \text{, contained in } F \} \right) \]

If we were talking about such a measure, then the inequality \( m_{*}(F) \ge m_{*,(J)}(F) \) would follow easily, as the collection of all countable box sets contained within some set \( F \subset \mathbb{R} \) includes all finite box sets. This progression of ideas is a symmetric match to how we arrived at \( m^*(F) \le m^{*,(J)}(F) \) above; however, it is not the inequality we are trying to prove.


So, remember then that we are comparing an outer measure (Lebesgue) with an inner measure (Jordan).

The back side of the card continues to explain the rightmost inequality.


Failed attempt (and motivation for Heine-Borel)

Trying to prove this inequality in the same way we thought about \( m^*(F) \le m^{*,(J)}(F) \) doesn't work:

Consider all finite sets of boxes that are contained within \( F \subset \mathbb{R}^d \). The volume of any of set union of these sets (i.e. the volume of any elementary set), must be less than the real \( m_{*,(J)}(F) \). Now consider any arbitrary set of boxes (including countably or uncountably infinite) contained within \( F \). Each of these sets has a finite subset whose union must have a volume less than \( m_{*,(J)}(F) \). Is this useful? No. \( m_{*, (J)}(F) \) is an upper bound and there is nothing (yet) preventing an infinite collection of boxes both covering \( F \) and having a volume less than \( m_{*, (J)}(F) \). Case in point: an uncountable set of boxes can have volume zero and cover \( F \). The fact that such a collection that has a finite sub-collection contained within \( F \) has no significance.

The question is: can we achieve the same zero-volume covering with just a countable set of boxes? If we can, then we can't make the assertion of the inequality: \( m_{*,(J)} \le m^*(F) \). However, it turns out we can't. And to show this, we need to draw on some fundamental qualities of compact spaces.

Why compactness comes into play

Consider the following chain of thought.

  • Try to cover an uncountable set in \( \mathbb{R}^d \) with boxes.
  • If we are allowed to use an arbitrary set of boxes, use uncountably infinite degenerate boxes with 0 volume.
  • But, now only countable boxes are allowed. If we can do it then...
  • The boxes can't all be zero volume anymore.
  • The boxes are (or are close enough to being) open sets. And the union of open sets is open.
  • \( F \) may not be closed, but consider any closed set \( D \) contained in \( F \). If our set of boxes covers \( F \), then it covers \( D \).
  • \( D \) is a closed set in a Hausdorff space, so it is compact and any open cover of \( D \) has a finite sub-cover.
  • So, we can cover \( D \) with a finite subset of our boxes.
  • Our box-cover of \( F \) must necessarily be larger than the finite box-cover of any closed \( D \subset F \).
  • And here's some magic. For any real \( V_E \) less than \( m_{*,(J)}(F) \) there is an elementary set \( E \) contained within \( F \) with volume \( V_E \). Any countable box-cover must cover \( E \) and must have a volume at least that of \( V_E \). So we can't cover \( F \) with a cover less than \( m_{*,(J)}(F) \).

In Tao's book, he first shows that \( m^{*}(E) = m(E) \) for an elementary set \( E \) with elementary measure \( m(E) \). There you can find a proper proof. From this result along with monoton

Countable boxes can't cover an elementary set with any less volume than a finite set of boxes

Can we cover an elementary set \( E \) with say uncountable boxes and get a smaller volume? Yes-cover each point with a zero volume box, for a total cover of zero volume.  So it's not a trivial fact that a countable set cannot improve upon a finite set. 

Can we cover an elementary set with countable boxes and get a smaller volume? No. Why? The reason stems from a box being compact (uncountably many yet bounded elements), and every open cover of a compact space has a finite sub-cover. The back side goes into more detail, but the gist is that no matter how we cover \( E \) with open boxes, there will be a finite set that also covers \( E \). A few details clean up cases where boxes are not open. So, we can't do better than a finite cover, and no set of boxes then can fit within \( F \) \( m_{*,(J)(F)} \) is the

An infinite box cover for an elementary set would allow for a cover consisting of closed, single element sets; the idea of a finite open cover from any open cover doesn't apply to a non-open cover, so it doesn't apply here.

Insight into uncountable box covers

It's interesting to take a detour to consider the exact same chain of thought, but starting from the set of arbitrary box covers for the set \( F \). We know that the union of boxes around each element of \( F \) is a cover for \( F \), and the total volume will be a sum of zero-volume boxes, making the total volume zero. This completes the zoo of possible outer measures when categorized as finite, countable and infinite.

Insert diagram for compactness.