\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Answer
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
Math and science::Analysis::Tao, measure::02. Lebesgue measure

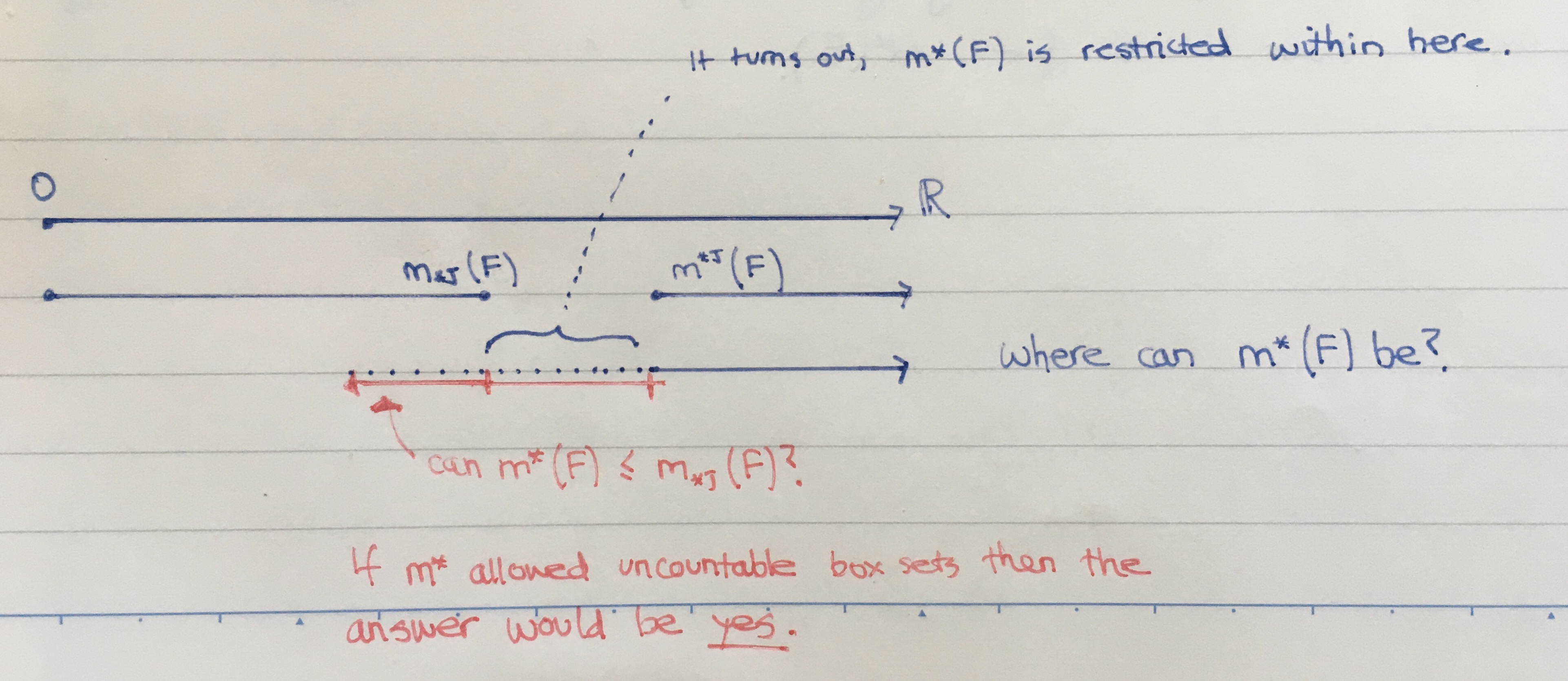
Lebesgue outer measure is between the Jordan inner and outer measures

This relation is useful to ground one's mental model of Lebesgue measure.

\[ m_{*,(J)}(F) \le m^*(F) \le m^{*,(J)}(F) \]

The proof outline for the rightmost inequality is simple. The leftmost inequality is not simple, it is somewhat profound.

1. Rightmost inequality, proof outline

\[ m^*(F) \le m^{*,(J)}(F) \]

In words: the Lebesgue outer measure is less-equal to the the Jordan outer measure.

Consider the set of all at-most-countable box covers for the set \( F \subset \mathbb{R}^d \); denote it by \( \mathcal{S} \). The real \( m^*(F) \) is the [something bound] for the volume of these covers. Contained as a subset off these covers is the set of all finite box covers; denote it as \( \mathcal{C} \). \( m^*(F) \) is a lower bound (the greatest) for \( \mathcal{S} \), so it must also be a lower bound for the subset \( \mathcal{C} \). The real \( m^{*,(J)}(F) \) is the greatest lower bound for \( \mathcal{C} \), so we have \( m^*(F) \le m^{*,(J)(F) } \).

2. Leftmost inequality. It's not trivial.

\[ m_{*,(J)}(F) \le m^*(F) \]

In words: the Lebesgue outer measure is not less than the Jordan inner measure.

The same logic as above seems to intuitively fit, but it doesn't.

Not a Lebesgue inner measure

Any finite set of boxes contained in \( F \) is not in the set of countable covers of \( F \). We are not comparing the Jordan inner measure \( m_{*,(J)}(F) \) to some countable extension. Such a real would be a supremum (not an infimum like the outer measure) and might look like:

\[ m_{*}(F) := \sup \left( \{ m \in \mathbb{R} : m = \sum_{b \in I} |b| \text{, for some countable collection of boxes, } I \text{, contained in } F \} \right) \]

If we were talking about such a measure, then the inequality \( m_{*}(F) \ge m_{*,(J)}(F) \) would follow easily, as the collection of all countable box sets contained within some set \( F \subset \mathbb{R} \) includes all finite box sets. This progression of ideas is a symmetric match to how we arrived at \( m^*(F) \le m^{*,(J)}(F) \) above; however, it is not the inequality we are trying to prove.


So, remember then that we are comparing an outer measure (Lebesgue) with an inner measure (Jordan).

The back side of the card continues to explain the rightmost inequality.