Closures, interiors and Jordan measure

- Proof outline: see other side
- Proof outline: see other side
- Proof outline: see other side
- Proof outline: see other side
(4), shows that Jordan outer measure (and inner measure) do not possess finite additivity for non-measurable sets. For the outer measure case, the question of what conditions might be needed to imply fintie additivity is partially answered by the Caratheodory type property.
The proofs below rely on the monotonicity of the Jordan inner and outer measure—two properties that Tao doesn't introduce explicitly. Tao does state the existence of monotonicity of both when the set being measured is Jordan measurabled.
1. \( E \) and the closure \( \overline{E} \) of \( E \) have the same Jordan outer measure.
Proof. Claim 1: \( m^{*,(J)}(E) \le m^{*,(J)}(\overline{E}) \). Claim 2: \( m^{*,(J)}(\overline{E}) \le m^{*,(J)}(E) \).
Claim 1, Jordan outer measure of a set is not greater than the outer measure of the set's closure. Proof. This follows from monotonicity of Jordan outer measure: any elementary set that contains \( \overline{E} \) must also contain \( E \), and so the infimum of elementary covers of \( \overline{E} \) cannot be less than the infimum of elementary covers of \( E \).
Claim 2, Jordan outer measure of a set's closure is not greater than the outer measure of the set itself. Proof. Consider any almost-disjoint elementary cover \( A \) of \( E \). If all boxes within \( A \) are replaced by closed boxes (so \( (1, 2] \) becomes \( [1, 2] \)), the measure doesn't change, so \( m(A) = m(\overline{A}) \). But \( E \subseteq A \implies \overline{E} \subseteq \overline{A} \). So \( \overline{A} \) is a cover of \( \overline{E} \) with the same measure as \( A \), our cover for \( E \). So \( m^{*,(J)}(\overline{E}) > m^{*,(J)}(E) \) is false, which proves the claim.
Any elementary set can be expressed as a finite union of disjoint boxes, so to consider the measure of an arbitrary disjoint cover is to consider the measure of any arbitrary cover.
2. \( E \) and the interior \( E^{\mathrm{o}} \) of \( E \) have the same Jordan inner measure.
The proof of this has a symmetry with the previous proof.
Proof. Claim 1: \( m_{*,(J)}(E^{\mathrm{o}}) \le m_{*,(J)}(E) \). Claim 2: \( m_{*,(J)}(E) \le m_{*,(J)}(E^{\mathrm{o}}) \).
Claim 1, Jordan inner measure of a set is not less than the inner measure of the set's interior. Just like the proof above, the first claim follows from monotonicity, this time the monotonicity of Jordan inner measure. As \( E^{\mathrm{o}} \subseteq E \), any set of boxes that fit in \( E^{\mathrm{o}} \) must also fit in \( E \), so it cannot be the case that \( m_{*,(J)}(E^{\mathrm{o}}) > m_{*,(J)}(E) \).
Claim 2, Jordan inner measure of a set is not greater than the inner measure of the set's interior. Consider any almost-disjoint set of boxes contained within \( E \). Replacing all boxes with open boxes (so \( [1, 2] \) becomes \( (1, 2) \)) doesn't change the elementary measure of the union of these boxes. As the union of open boxes is open, they all fit within the interior \( E^{\mathrm{o}} \); and so the supremum of elementary sets that fit in \( E^{\mathrm{o}} \) cannot be less than the supremum of elementary sets that fit in \( E \). In other words, it is true that \( m_{*,(J)}(E) \le m_{*,(J)}(E^{\mathrm{o}}) \).
3. \( E \) is Jordan measurable iff the topological boundary \( \partial E \) of \( E \) has Jordan outer measure zero.
Forward implication proof. Assume that \( E \) is Jordan measurable. If \( E \) is Jordan measurable, then all of the following four quantities are equal:
The inner equality is true by the definition of Jordan measurability, and the two outer equalities hold by the two statements that were proven above.
Applying monotonicity of inner and outer measure we conclude that both \( E^{\mathrm{o}} \) and \( \overline{E} \) are Jordan measurable. With both being Jordan measurable, we can utilize the finite additivity of disjoint Jordan measurable sets: \[ E^{\mathrm{o}} \cap \partial E = \emptyset \implies m(E^{\mathrm{o}} \cup \partial E) = m(E^{\mathrm{o}}) + m(\partial E) \] But \( E^{\mathrm{o}} \cup \partial E = \overline{E} \) and \( m(E^{\mathrm{o}}) = m(\overline{E}) \), so \( m(\partial E) = 0 \). This is sufficient (and actually stronger) than our claim that the outer measure of the boundary is zero.
Reverse implication proof. Assume that \( m^{*,(J)}(\partial E) = 0 \) [STUCK!].
Lemma. \( m_{*,(J)}(E) \ge m^{*,(J)}(E^{\mathrm{o}}) \), Jordan inner measure of \( E \) cannot be less than the Jordan outer measure of \( E^{\mathrm{o}} \). This can be shown by utilizing the contract boxes to be open trick from before. We can use \( m_{*,(J)}(E) \) to produce an elementary set contained in \( E \), then create another elementary set with the same volume by utilizing open disjoint boxes. This latter elementary set, being open, must be within \( E^{\mathrm{o}} \) and must have a volume less than \( m^{*,(J)}(E^{\mathrm{o}} \). , By utilizing the sub-additivity of outer Jordan measure we have \( m^{*,(J)}(E^{\mathrm{o}} \cup \partial E) \le m^{*,(J)}(E^{\mathrm{o}}) + m^{*,(J)}(\partial E) \), but by assumption, \( m^{*,(J)}(\partial E) = 0 \), so that \( m^{*,(J)}(E^{\mathrm{o}} \cup \partial E) \le m^{*,(J)}(E^{\mathrm{o}}) \), \( \mathrm{o} \cup \partial E = \overline{E} \), so the inequality can be expressed as \( m^{*,(J)}(E^{\overline{E}}) \le m^{*,(J)}(E^{\mathrm{o}}) \). The inner measure \( m_{*,(J)}(\overline{E}) \) must always be greater than the outer measure \( m^{*,(J)}(E^{\mathrm{o}}) \), else we would be able to find a finite box cover containing \( \overline{E} \) that has a smaller volume than some finite box cover contained within...
So, I'm stuck on this proof.
Visually, monotonicity and sub-additivity gives us the following situation:
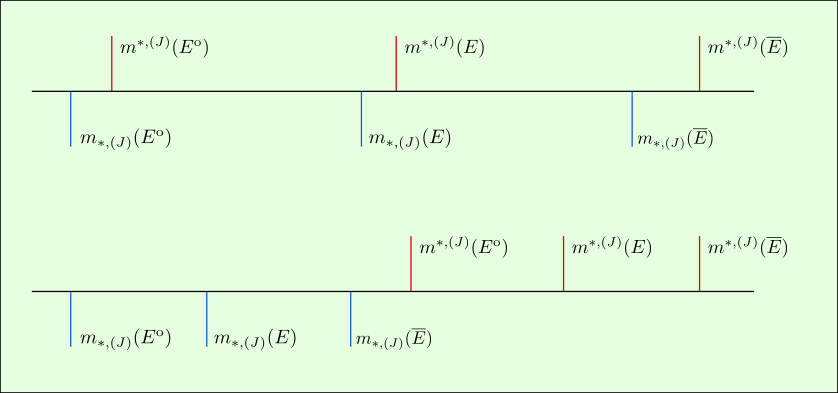
And the ability to convert covers to be open or closed gives us the following situation:
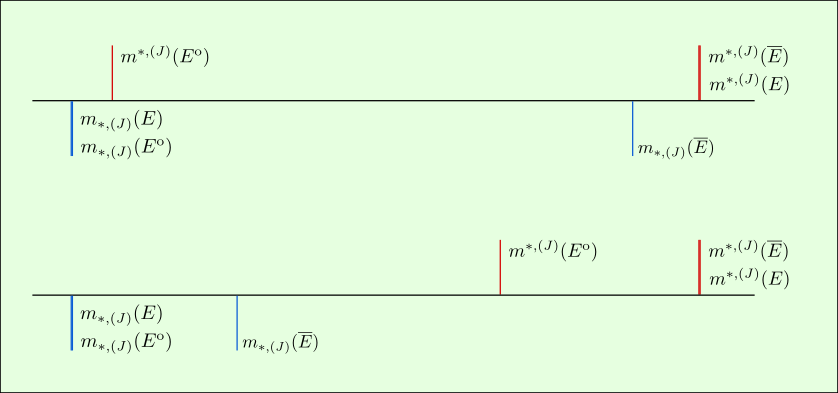
Using the assumption about zero outer measure for the boundary, we can apply sub-aditivity of the outer and inner measures again. This squashes all outer measures together and all inner measures together:

But I'm not sure how to get to this:

4. Jordan measure of the bullet-riddled square and the set of bullets
The closure of the rationals is the reals, and the closure of the reals minus the rationals is the reals. So the outer measure of both sets is the reals, in this case just the subset \( [0, 1] \). There is no open set (no interval of \( \mathbb{R} \)) that doesn't contain a rational, so the interior of the bullet-riddled square is the empty interval. Similarly, there are no open sets that contain only rationals, so the interior of the bullets is also the empty set.
The Jordan outer measure of both sets is equal to the outer measure of \( [0, 1] \) and the Jordan inner measure of both sets is equal to the inner measure of \( [0,0] \). These measures are 1 and 0 respectively.
