\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
Math and science::Analysis::Tao, measure::01. Jordan measure

Carathéodory type property

Let \( E \subset \mathbb{R}^d \) be a bounded set, and let \( F \subset \mathbb{R}^d \) be an elementary set. It is true that:

\[ m^{*,(J)}(E) = m^{*,(J)}(E \cap F) + m^{*,(J)}(E \setminus F) \]

Proof outline

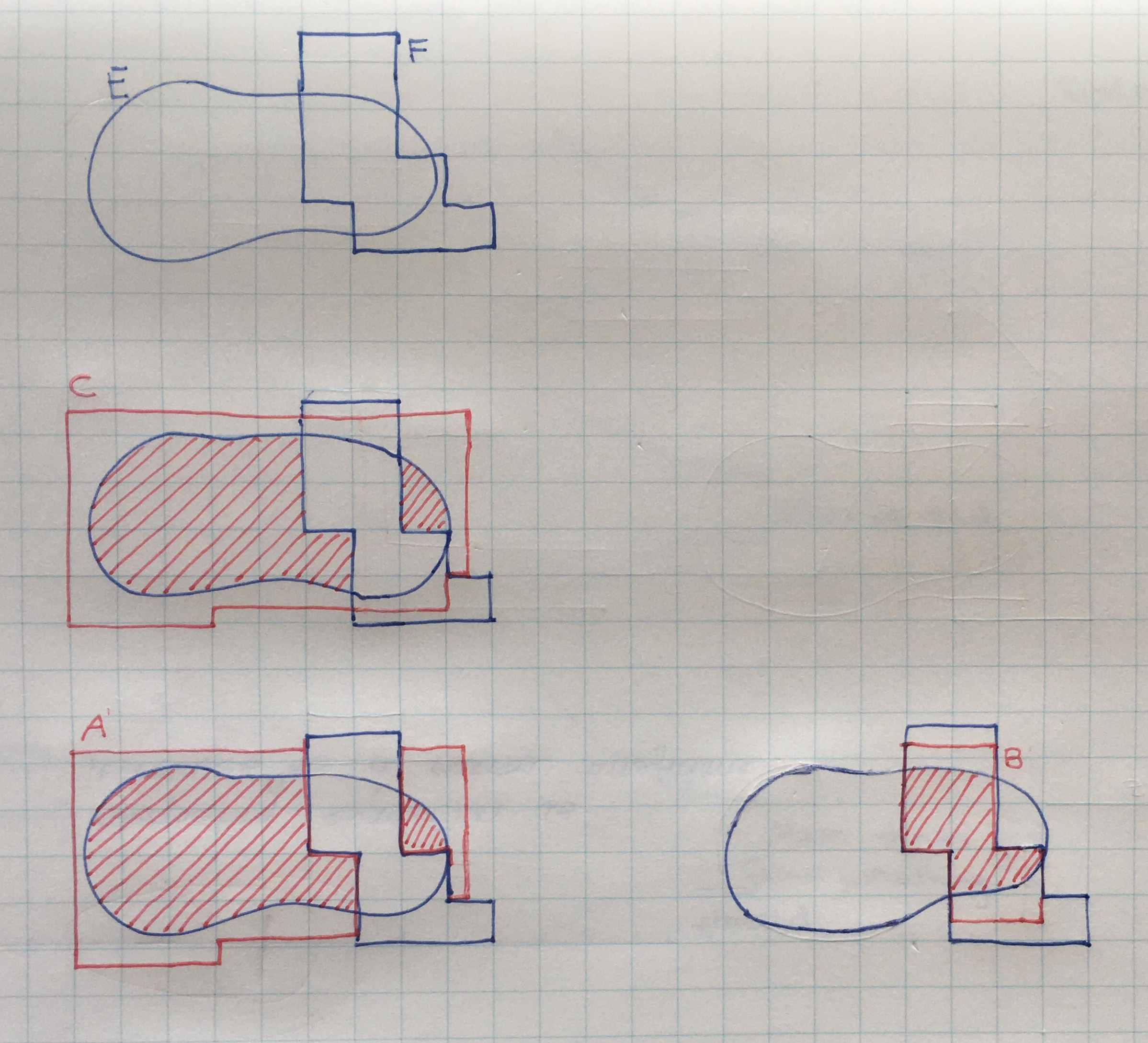
An elementary cover \( C \) of a set \( E \) can be broken into two disjoint elementary sets, \( A \) and \( B \) which union to \( C \). This can be done by taking the intersection and difference of \( C \) with some other elementary set \( F \). \( A \) will be a cover for \( E \setminus F \) and \( B \) a cover for \( E \cap F \). As \( A \) and \( B \) are disjoint, we have \( m(A \cup B) = m(A) + m(B) \). \( A \) and \( B \) will have an elementary measure larger than the infimum representing \( m^{*,(J)}(E \setminus F) \) and \( m^{*,(J)}(E \cap F) \) respectively, however, they will have a summed measure smaller than that of \( C \) which can be made arbitrarily close to \( m^{*,(J)}(E) \).

Implication

In this formulation, the Carathéodory type property can be thought of as being one answer to the question: under what conditions do we have finite additivity of outer Jordan measure (not mere sub-additivity)? 

This question is especially pertinent when considering the fact that Jordan outer measure, while additive for Jordan measurable sets, is not additive in general: the outer measure of the union of the bullets and the bullet-riddled square is 1 (as union is \( [0,1] \)), yet the outer measure of each set individually is also 1.

The answer is that if a set \( E \) is split by an elementary set into \( A \) and \( B \), then any cover of \( E \) can be split (without repeat) and cover \( A \) and \( B \). This makes \( m^{*,(J)}(A) + m^{*,(J)}(B) \le m^{*,(J)}(E) \). The reverse inequlity is simply the characteristic of sub-additivity, which is indeed possessed by outer measure.

Proof

For any real \( \delta > 0 \) there exists an elementary set \( C \) covering \( E \) with elementary measure \( m(C) \le m^{*,(J)}(E) + \delta \). \( C \) can be broken into two disjoint elementary sets \( A = C \setminus F \) and \( B \cap F \) for some elementary set \( F \), and we will have \( m(C) = m(A) + m(B) \). This means that \( m(C) = m(A) + m(B) \le m^{*,(J)}(E) + \delta \). It is true (can be checked with some set algebra) that \( A \) is a cover for \( E \setminus F \) and \( B \) a cover for \( E \cap F \). Consequently, \( m(A) \ge m^{*,(J)}(E \setminus F) \) and \( m(B) \ge m^{*,(J)}(E \cap F) \). Substituting this back into the previous inequality we see that:

\[ m^{*,(J)}(E \setminus F) + m^{*,(J)}(E \cap F) \le m^{*,(J)}(E) + \delta \]

\( \delta \) was arbitrary so we can say:

\[ m^{*,(J)}(E \setminus F) + m^{*,(J)}(E \cap F) \le m^{*,(J)}(E) \]

That proves the harder of the two inequalities needed! Paired with the sub-additivity of outer Jordan measure, we have equality:

\[ m^{*,(J)}(E \setminus F) + m^{*,(J)}(E \cap F) = m^{*,(J)}(E) \]