\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
Math and science::Analysis::Tao, measure::02. Lebesgue measure

Outer Lebesgue measure of countable union of almost disjoint boxes

If a set is expressible as a countable union of almost disjoint boxes, then what is it's outer Lebesgue measure?

Outer Lebesgue measure of countable union of almost disjoint boxes

Let \( E = \bigcup_{n=1}^{\infty} B_n \) be a countable union of almost disjoint boxes. Then

\[ m^*(E) = \sum_{n=1}^{\infty}|B_n| \]

What else equals the RHS above? We can say the following:

For a countable union of disjoint boxes, the Lebesgue outer measure is equal to the Jordan inner measure.


Outer Lebesgue measure of countable union of almost disjoint boxes. Proof

Claim 1: \( m^*(E) \le \sum_{n=1}^{\infty}|B_n| \). Proof. This follows from countable sub-additivity:

\[ m^*(E) \le \sum_{n=1}^{\infty} m^*(B_n) = \sum_{n=1}^{\infty}|B_n| \]

The right equality follows from the Lebesgue outer measure of a box being the box's volume (Lemma 1.2.6 by Tao. Covered by another Anki card). It's interesting to note here that Jordan outer measure could not make this claim.

Claim 2: \( m^*(E) \ge \sum_{n=1}^{\infty}|B_n| \). Proof. For any natural \( N > 0 \), \( B_1 \cup ... \cup B_N = \bigcup_{n=1}^{N} B_n \) is a subset of \( E \). So, by monotonicity of Lebesgue outer measure, \( m^*(E) \ge m^*(\bigcup_{n=1}^{N} B_n) \); and by Lemma 1.2.6 \( m^*(\bigcup_{n=1}^{N} B_n) = m(\bigcup_{n=1}^{N} B_n) \); finally, this means that \( m^*(\bigcup_{n=1}^{N} B_n) \ge \sum_{n=1}^{N} |B_n| \), as the boxes are all disjoint, making the Jordan measure equal the sum of the box volumes. This is true for all \( N \), and taking the limit as \( N \to \infty \) we arrive at the real:

\[ \lim_{n \to \infty} \sum_{n=1}^{N}|B_n| = \sum_{n=1}^{\infty}|B_n| \]

Lebesgue outer measure equals Jordan inner measure (for countable almost disjoint boxes). Proof.

Let \( E = \bigcup_{n=1}^{\infty} B_n \) be a countable union of disjoint boxes. From above, we know that \( m^*(E) = \sum_{n=1}^{\infty} |B_n| \). Claim: \( m_{*,(J)}(E) = \sum_{n=1}^{\infty}|B_n| \). The limit of a monotone increasing sequence is its supremum (note that \( m_{*,(J)}(E) \) is a supremum), and as box volumes are always positive we must have

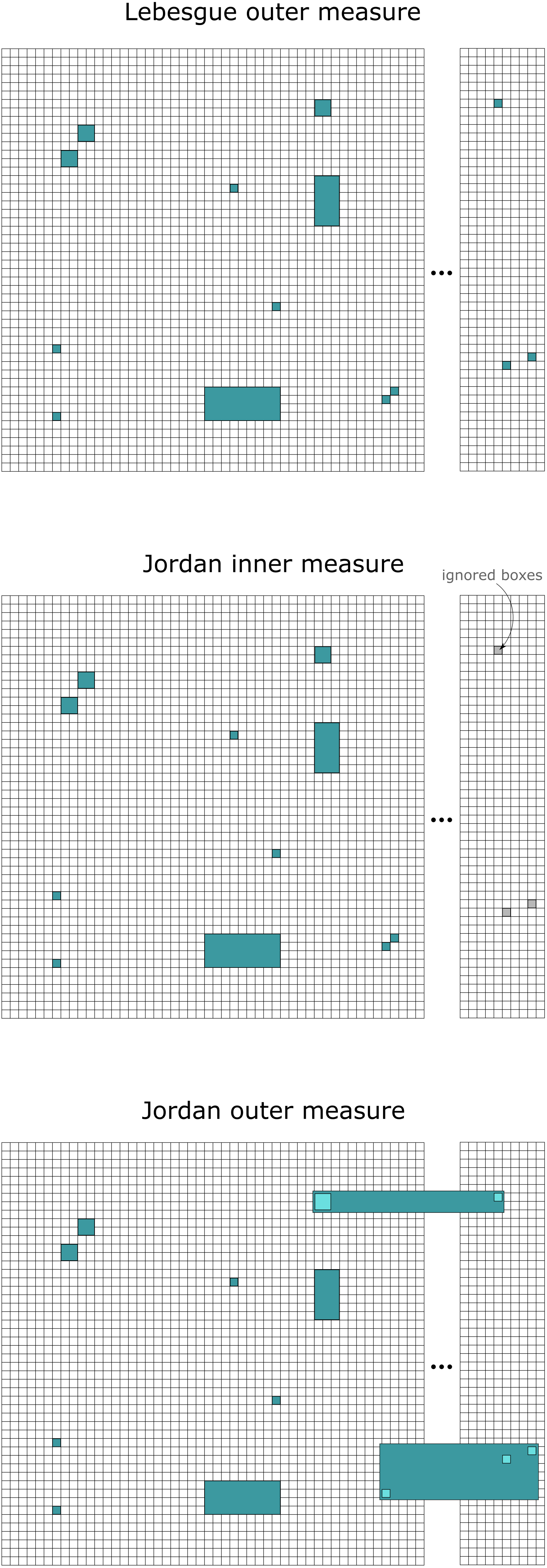
\[ m_{*,(J)}(E) = \lim_{N \to \infty} \sum_{n=1}^{N} |B_n| = \sum_{n=1}^{\infty} |B_n| \]

Visual intuition

Below is visual justification for why a countable union of disjoint boxes has a Jordan inner measure and Lebesgue outer measure which are equal and finite, yet it doesn't necessarily have a finite Jordan outer measure.

  • The Lebesgue outer measure can cover the countably infinite boxes with a 1-1 cover (for every box, cover the box with itself).
  • The Jordan inner measure is the limit as the number of finite boxes being filled approaches infinity. Effectively, the Jordan inner measure can be imagined to ignore filling in a countable number of boxes yet incur an arbitrarily small loss of volume compared to the Lebesgue outer measure.
  • The Jordan outer measure can't 'ignore' any boxes: it must cover the whole set.

A case where the Jordan outer approaches infinity yet the Jordan inner measure converges is where there is an infinite number of boxes spaced evenly apart in a line with decreasing volume, say \( |B_n| = \frac{1}{n^2} \)). The Jordan inner measure will represent a convergent limit of filling in these boxes, whereas the Jordan outer measure will be forced to cover an infinite volume.

Source

p23