Math and science::Analysis::Tao, measure::02. Lebesgue measure

Lebesgue measurable sets.

The following sets meet the criteria to be Lebesgue measurable:

Every open set is Lebesgue measurable.
A countable union of Lebesgue measurable sets is Lebesgue measurable.
Every closed set is Lebesgue measurable.
The complement $R^{d} ∖ E$ of a Lebesgue measurable set $E$ is Lebesgue measurable.
A countable intersection of Lebesgue measurable sets is Lebesgue measurable.

Two others are:

Every set of Lebesgue outer measure zero is measurable. These sets are called null sets.
The empty set $\emptyset$ is Lebesgue measurable.

The proofs are on the reverse side, along with a repeat of the definition of Lebesgue measurability.

Definition recap.

Lebesgue measurability. Definition.

A set $E \subset R^{d}$ is said to be Lebesgue measurable iff for every real $ε > 0$ there exists exists an open set $U \subset R^{d}$ containing $E$ such that $m^{*} (U ∖ E) \leq ε$ . If $E$ is Lebesgue measurable, we refer to $m (E) := m^{*} (E)$ as the Lebesgue measure of $E$ .

The proofs are below. We start with the easier ones.

Every set with Lebesgue outer measure zero is measurable. Proof.

Let $E \subset R^{d}$ be a set with $m^{*} (E) = 0$ . Recall that outer regularity allows allows us to choose, for any $ε > 0$ , an open set $O$ that contains $E$ and has measure $m^{*} (O) < m^{*} (E) + ε$ . As $m^{*} (E) = 0$ , this means $m^{*} (O) < ε$ . We are free to choose $ε$ and so, the measurability criteria above is easily met.

The empty set $\emptyset$ is Lebesgue measurable. Proof.

This follows from the above proposition. Alternatively, repeat the idea of the previous proof for the specific case of $\emptyset$ .

1. Every open set is Lebesgue measurable. Proof.

This proposition it follows directly from the definition. Any open set has itself as a set which can be used to satisfy the criteria.

2. A countable union of Lebesgue measurable sets is Lebesgue measurable. Proof.

This proof uses a classic application of the $\frac{ε}{2^{n}}$ trick. Let $E = \cup_{i = 1}^{\infty} E_{i}$ be the countable union of measurable sets, $E_{1}, E_{2}, . . .$ . Let $ε > 0$ be a real. For every $E_{i}$ , choose an open set $O_{i}$ with $E_{i} \subset O_{i}$ and $m^{*} (O_{i} - E_{i}) < \frac{ε}{2^{i}}$ . Then consider the sum of these open sets: $O = \cup_{i = 1}^{\infty} O_{i}$ . $O$ is open, $E \subset O$ and $O - E \subset \cup_{i = 1}^{\infty} O_{i} - E_{i}$ . By monotonicity and sub-additivity we have:

m^{*} (O - E) \leq \sum_{i = 1}^{\infty} m^{*} (O_{i} - E_{i}) \leq \sum_{i = 1}^{\infty} \frac{ε}{2^{i}} = ε

The reasoning behind the next 2 propositions is a bit more involved.

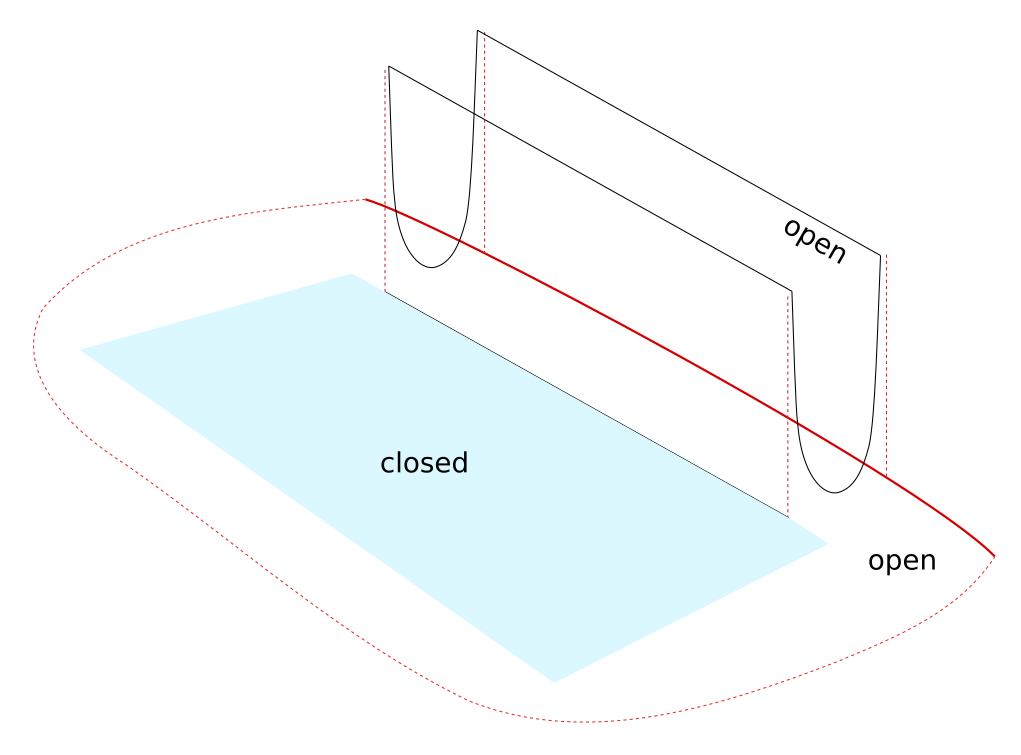
3. Every closed set is Lebesgue measurable. Proof.

Proof essence: consider a closed compact set. We can cover it with an open set with just $ε$ extra measure. An open set minus a closed set is open. The remaining space within the open set but not in the closed set ends up having at most $ε$ measure, as we can approximate it by finite disjoint boxes which are also disjoint from the closed set (we are able to apply finite additivity).

Refer to Tao or Stein for the detailed proof. The following diagram tries to evoke some intuition behind the reasoning.

4. The complement $R^{d} ∖ E$ of a Lebesgue measurable set $E$ is Lebesgue measurable. Proof.

The proof of this proposition involves approximating the complement from within by closed sets, then noting that the left over space has measure zero, and then the complement is measurable as closed sets are measurable and so too is any set with measure zero.

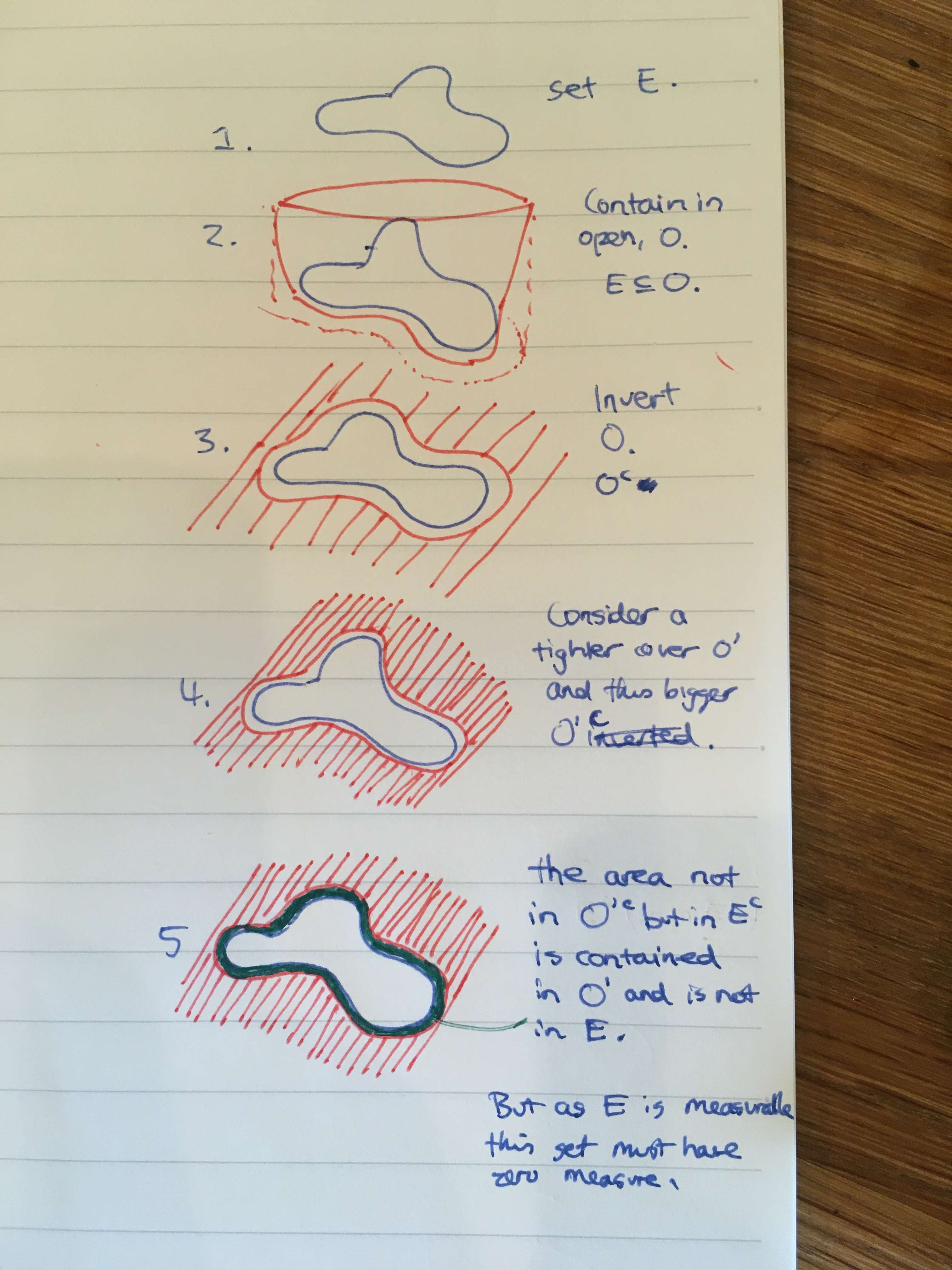
Proof. Let $E$ be measurable. For every $n \subset N$ we choose an open set $O_{n}$ containing $E$ such that $m^{*} (O_{n} - E) \leq \frac{1}{n}$ . The complement $O_{n}^{c}$ of each set is closed, and the union of all of them, $S = \cup_{i}^{n} O_{n}^{c}$ is measurable (it's a union of measurable sets). Now consider the set $E^{c} - S$ . Elements of this set are in $E^{c}$ and not in $S$ , so they are not in $E$ and are in every $O_{n}$ . In other words:

E^{c} - S \subseteq O_{n} - E, for any n > 0

By monotonicity, we have:

m^{*} (E^{c} - S) \leq m^{*} (O_{n} - E) \leq \frac{1}{n}, for all n}

Therefore $m^{*} (E^{c} - S) = 0$ , and $E^{c} - S$ is measurable (all sets with outer Lebesgue measure zero are measurable–see above). Now note that $E^{c} = S \cup (E^{c} - S)$ , both of which sets are measurable, so $E^{c}$ must also be measurable, as it is the union of two measurable sets.

The following diagram tries to stimulate some visual intuition for these steps.

5. A countable intersection of Lebesgue measurable sets is Lebesgue measurable.

This follows from the measurability of the complement of a countable union of measurable sets.

Source

Stein, p16

Tao, p26

04.11.2020