deepdream of a sidewalk
Show Question
Math and science::Analysis

The Cantor Set

The Cantor set is important for understanding Topology (open and closed sets) and measure.

Cantor set

Let C0 be the closed interval [0,1] and define C1 to be the set that results when the open middle third is removed:

C1=C0∖(13,23)=[0,13]∪[23,1]

This process continued gives us the Cantor set:

C=⋂n=0∞Cn
Or alternatively:
C=[0,1]∖((13,23)∪(19,29)∪(79,89)∪...) \]


Properties of the Cantor set

Below are some properties of the Cantor set, with explanations on the reverse side.

The cantor set...

  • has zero measure
  • is uncountably infinite
  • has dimension of 23
  • is closed
  • is compact
  • is perfect
  • is nowhere dense


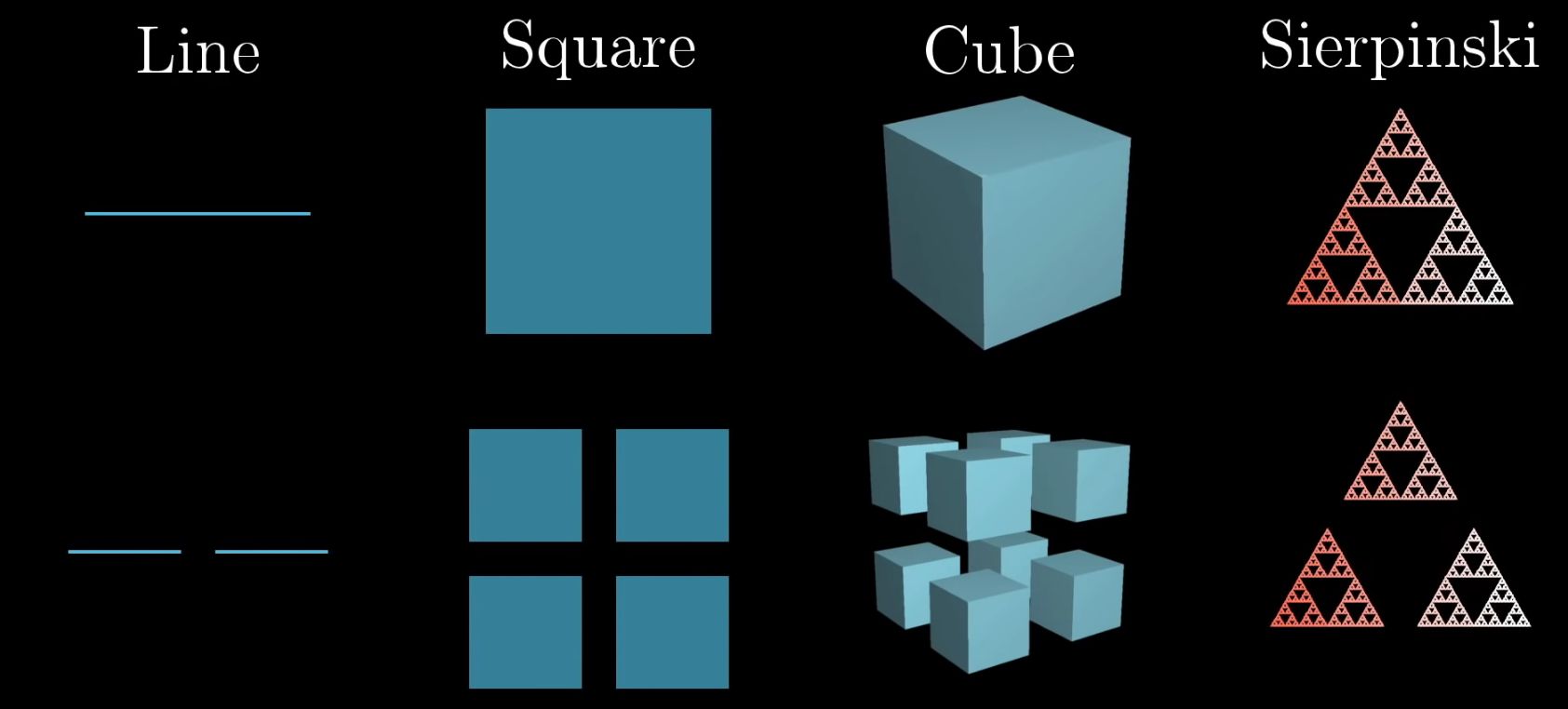
Dimension 23

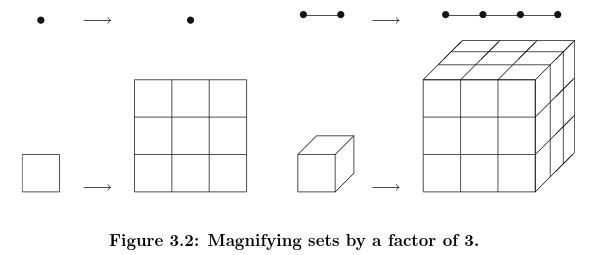
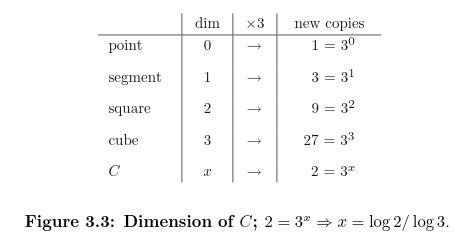
Scaling the Cantor set by 3 makes 1 copy into 2 copies of the set. If the dimension of a set is defined as being the exponent by which a scaling is raised to to count the number of copies, then the Cantor set has a dimension of 23. In other words, 3d=2⟹d=23.

Consider the set [0,1], and magnify it three times to produce [0,3]. When beginning the construction of the Cantor set on the set [0,3], we come upon C1=[0,1]∪[2,3], which contains two copies of the original set (and therefore will produce two copies of the Cantor set, with the following step in the construction being equivalent to the first step of the construction of the Cantor set in both [0,1] and [2,3]. Therefore, if the Cantor set has dimension x, then 2=3x, and x=0.63.