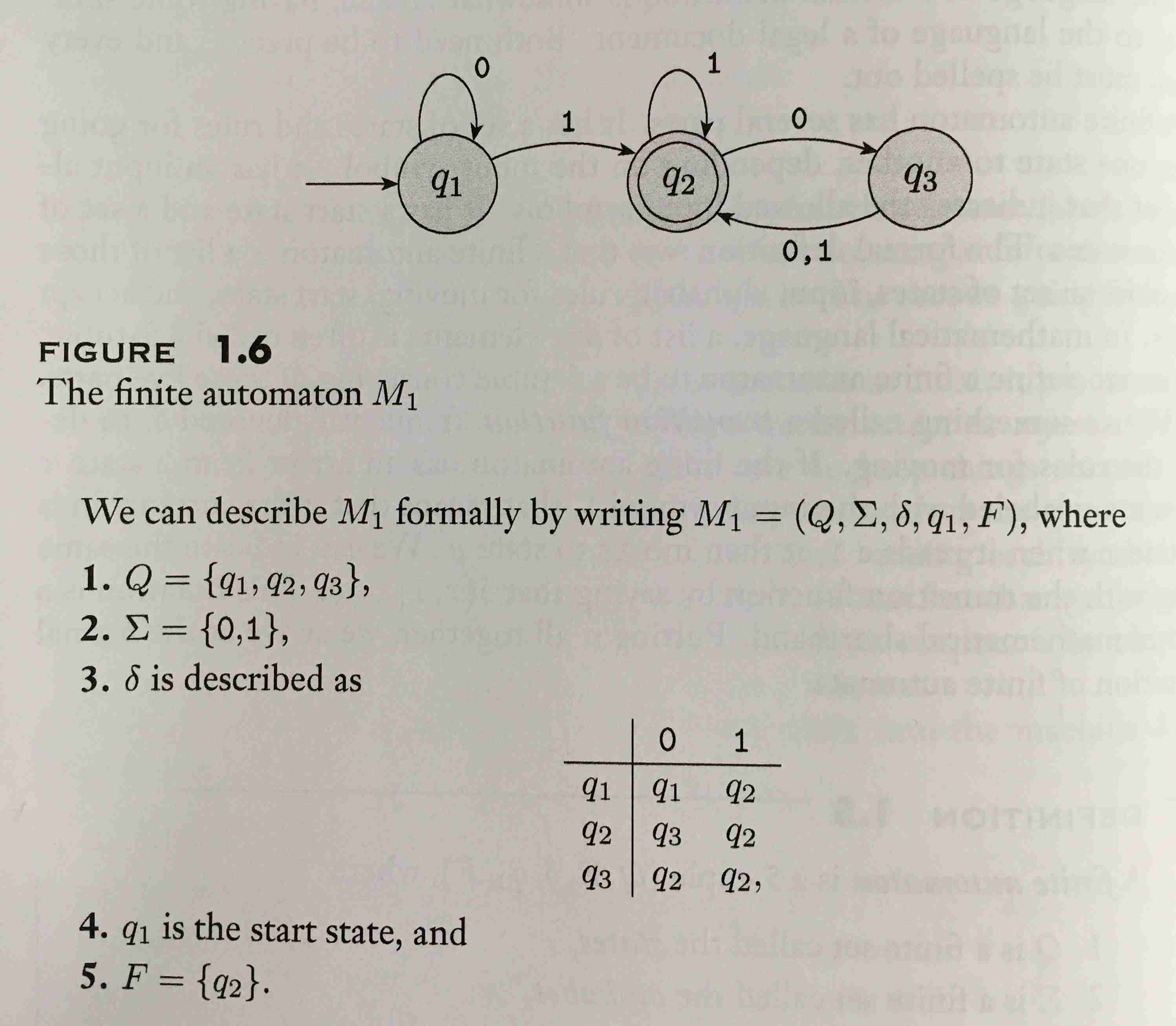Finite automata
A finite automaton (plural: automata) is a model of computation. Finite automata and their probabilistic counterpart Markov chains are useful tools when attempting to recognize patterns in data. Their formal definition has a 1-1 correspondence with a type of state diagram.
A finite automaton is a 5-tuple (\( Q, \Sigma, \delta, q_0, F \)), where:
- \( Q \) is a finite set called the states,
- \( \Sigma \) is a finite set called the alphabet,
- \( \delta : Q \times \Sigma \to Q \) is the transition function,
- \( q_0 \in Q \) is the start sate, and
- \( F \subseteq Q \) is the set of accept states.
Processing of input
When an automaton receives an input string, it can either accept or reject it. A string is accepted if the automaton is in an accept state once the full input string is processed. Formally this is described as:
String acceptance
Let \( M = (Q, \Sigma, \delta, q_0, F) \) be a finite automaton and let \( w = w_1w_2...w_n \) be a string where each \( w_i \) is a member of the alphabet \( \Sigma \). Then \( M \) accepts \( w \) iff a sequence of states \( r_0, r_1, ..., r_n \) is \( Q \) exists with three conditions:
- \( r_0 = q_0 \)
- \( r_{i+1} = \delta(r_i, w_{i + 1}) \text{ for } i = 0, ..., n - 1\), and
- \(r_n \in F \)
\( w \) is rejected iff it is not accepted.
If \( A \) is the set of all strings that machine \( M \) accepts, we say that \( A \) is the language of machine \( M \) and write \( L(M) = A \). We say that M recognizes A.
State machine representation
A finite automaton has a 1-1 correspondence with a graphical state machine representation.