\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
Math and science::Theory of Computation

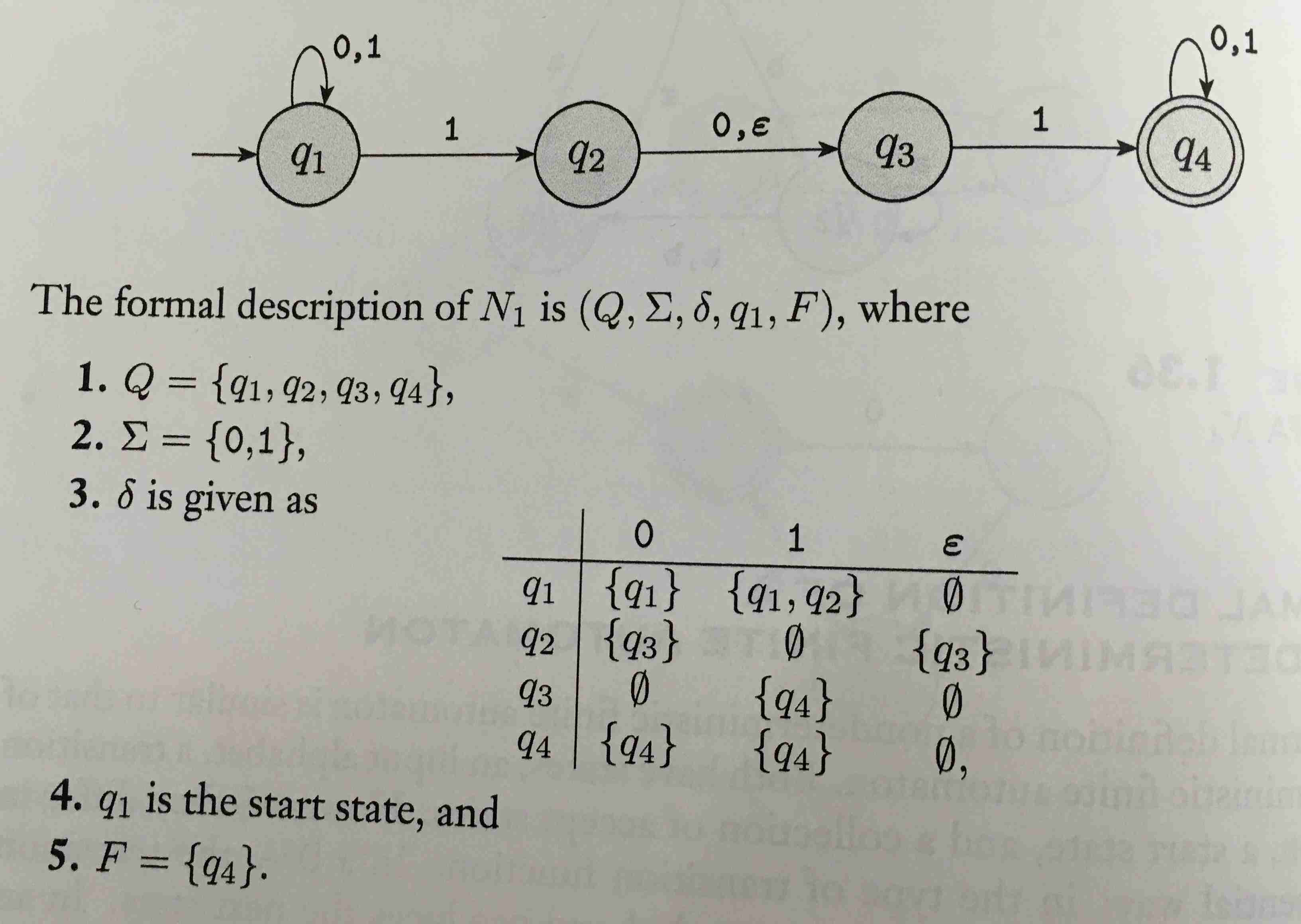
Nondeterministic finite automata (NFA)

Nondeterministic finite automata definition

A nondeterministic finite automaton is a 5-tuple \( (Q, \Sigma, \delta, q_0, F) \), where

  1. \( Q \) is a finite set called the states,
  2. \( \Sigma \) is a finite set called the alphabet,
  3. \( \delta : Q \times \Sigma_{\varepsilon} \to 2^Q \) is the transition function,
  4. \( q_0 \in Q \) is the start sate, and
  5. \( F \subseteq Q \) is the set of accept states.

String acceptance

Let \( M = (Q, \Sigma, \delta, q_0, F) \) be a NFA, let \( w \) be a string over the alphabet \( \Sigma \), and let \( \Sigma_{\varepsilon} = \Sigma \cup \{\varepsilon\} \) (where \( \varepsilon \) represents the empty string).

Then \( M \) accepts \( w \) iff we can write \( w = y_1y_2...y_m \) where \( y_i \in \Sigma_{\varepsilon} \) and there exists a sequence of states in \( Q \), \( r_0, r_1, ..., r_m \), meeting three conditions:
  1. \( r_0 = q_0 \)
  2. \( r_{i+1} \in \delta(r_i, y_{i+1}) \text{, for } i = 0, ..., m-1 \)
  3. \( r_m \in F \)

\( w \) is rejected iff it is not accepted.

Every nondeterministic finite automaton has an equivalent deterministic finite automaton (two machines are equivalent iff they recognize the same language). The proof of this is worth studying.


Viewed from the perspective of a state machine, nondeterministic finite automata depart from deterministic finite automata by:

  1. allowing multiple transitions out of a state for a single symbol in the alphabet.
  2. introducing the automatic transitions, denoted with \( \varepsilon \).
  3. their parallel computation and acceptance.

Proof outline of NFA an DFA equivalence

Let \( N = (Q, \Sigma, \delta, q_0, F) \) be the NFA recognizing some language \( A \). Try to construct a DFA \( M = (Q', \Sigma, \delta', q_0', F') \) that is equivalent to \( N \).

Construction

States

\( Q' = 2^Q \)

If a DFA is to keep track of the computation of an NFA, it must keep track of all possible active states of the NFA. If an NFA has \( k \) states, an equivalent DFA needs to have \( 2^k \) states, one state for every subset of the NFA's states.

Note how the elements of \( Q' \) are sets! This must be understood in order to make sense of the transition function.

Transitions

For \( R \in Q' \) and \( a \in \Sigma \), let \( \delta'(R, a) = \{q \in Q \mid q \in \delta(r, a) \text{ for some } r \in R \} \)

The transition function for M maps a subset of states of N to a subset of states of N.

Start state
\( q_0' = {q_0} \). Note that for the DFA, the state is a set.
Accept states
\( F' = \{ R \in Q' \mid R \text{ contains an accept state of N}  \} \)

A tweak of the transition function described above is needed to account for the \( \varepsilon \) transitions.

Example

Source

Introduction to the Theory of Computation, Sipser
p48-55