Turing-recognizable and Turing-decidable
The following four propositions are true:
Every Turing-decidable language is Turing-recognizable.
There exist Turing-recogniziable languages that are not Turing-deciable.
Every language can be recognized by multiple turing machines.
There does exist languages which are not Turing-decidable. There does exist languages that are not Turing-recognizable.
Every Turing machine has a language that it recognizes.
See the back for some explanations. The rest of this card builds up terminology used in the above propositions.
The concepts of recognizable and decidable rely on the concept of a configuration. The initial state of a Turing machine is typically described by a 7-tuple, but while operating, the head will move, and the tape will change, and a configuration is used to specify the current state of the tape and head.
Configurations
The tuple (FSM state, tape contents, tape head position) is called a configuration. Configurations are often written like so: 1011q701111. This configuration represents a Turing machine with the the following state:
- the tape contents is '101101111'
- the state machine's state is q7
- the head is at position 4 (over the rightmost 0).
Accept, reject or loop
The essence of the Turing machine is captured in the transition function, \( \delta \), as it shows how and with what limits the machine can change from state to state.
There are three outcomes possible after starting a Turing machine on an input:
- the machine may end and accept the input string by entering state \( q_{accept} \),
- the machine may end and reject the input string by entering state \( q_{reject} \),
- or the machine may never end.
Comparison to finite automata
A noteworthy difference between Turing machines and finite automata is that finite automata stop once they have consumed the whole input. Turing machines can continue indefinitely after passing over all or only part of the input.
Languages reconized by a Turing machine
Let \(M = (Q, \Sigma, \Gamma, \delta, q_{accept}, q_{reject}) \) be a Turing machine. The collection of strings that \( M \) accepts is called the the language recognized by \( M \), or simply the language of \( M \), denoted \( L(M) \).
An alternative description of the above concept highlights the nature of the correspondence:
TM M recognizes language L iff:
- The strings in L put M into the accept state.
- The strings NOT IN L either:
- put M into the reject state, or
- cause M to loop.
The second type of language associated with a Turing machine:
Languages decided by a Turing machine
Let \(M = (Q, \Sigma, \Gamma, \delta, q_{accept}, q_{reject}) \) be a Turing machine that always halts (never loops). The collection of strings that \( M \) accepts is called the the language decided by \( M \).
Categorizing languages
Any language can be categorized as to whether there exists a Turing machine that recognizes it or not; similarly, all languages can be categorized as to whether there exists a Turing machine that decides it.
A language is called Turing-recognizable iff some Turing machine recognizes it.
Alternative terminology for Turing-recognizable language: recursively enumerable language.
A language is called Turing-decidable (or just decidable) iff some Turing machine decides it.
Alternative terminology for Turing-decidable language: recursive language.
Visualizing the space of languages divided by a Turing machine
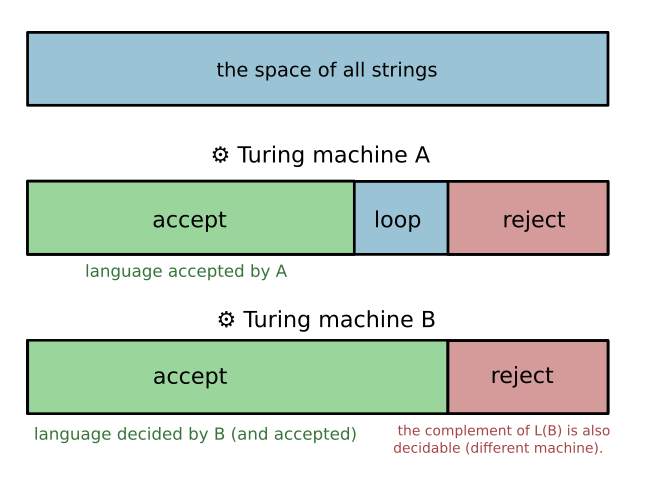
Every decidable language is Turing-recognizable. Explanation.
Take any decidable language. By definition, there is a Turing machine that decides it. Replace all reject states with accept states [this sounds wrong....]. Now you have a Turing machine that accepts every string in the language. The reverse is not true. It is true that there exists languages that are recognizable but not deciable! See: this explanation, or the attached pdf (downloaded from here).
Multiple Turing machines per language. Explanation.
While each Turing machine has only 1 language that it recognizes and 1 language that it decides, a language can have multiple Turing machines that recognize or decide it. To see this, imagine making a change to a Turing machine that has no effect, like adding a state that is never reached.
Undecidable, unrecognizable
There are uncountably many languages, but only countable many Turing machines. As each Turing machine can only recognize a single language, there must be languages for which no Turing machine recognizes. Such languages are also not decided by any Turing machine.
A recognizer or a decider
A Turing machine can either recognize a lanugage decide a language, but not both. If there is any string for which the Turing machine doesn't halt, then that machine cannot decide any language. So a Turing machine is either a recognizer or a decider!
Turing machine, recap
A recap, below is a formal definition of a Turing machine:
Turing machine
A Turing machine is parameterized as a 7-tuple, \( (Q, \Sigma, \Gamma, \delta, q_{accept}, q_{reject}) \), where \( Q, \Sigma \) and \( \Gamma \) are all finite sets, \( \delta \) is a function and \( q_{accept} \) and \( q_{reject} \) are elements of \( \Sigma \).
- \( Q \) is the set of states of the machine's underlying finite state machine.
- \( \Sigma \) is the input alphabet. It doesn't contain the {{c1::blank symbol, ␣}}.
- \( \Gamma = \Sigma \cup \{␣\} \) is {{c1::the tape alphabet::what alphabet?}}.
- {{c1::\( \delta : Q \times \Gamma \to Q \times \Gamma \times \{L, R\} \)::\( \delta : Q \times ? \to ? \times ? \times ? \)}} is the transition function.
- \( q_0 \in Q \) is the start state.
- \( q_{accept} \in Q \) is {{c1::the accept state::what?}}.
- \( q_{reject} \in Q \) is {{c1::the reject state::what?}}, where \( q_{reject} \ne q_{accept} \).
The above 7-tuple describes the initial conditions of a Turing machine.
