β-reduction
Beta reduction is a term that encompasses 3 relations defined over the set of all lambda terms: single-step, multi-step and equality.
β-reduction, single step, \( \rightarrow_{\beta} \)
Let \( M, U \) and \( L \) be lambda terms.
The following 2 rules define the true entries of the single step beta reduction relation.
- Basis
- \( (\lambda .\, M) U \rightarrow_{\beta} M[x :=U] \)
- Compatibility
- If \( M \rightarrow_{\beta} U \), then:
- \( ML \betaReduction UL \)
- \( LM \betaReduction LU \)
- \( \lambda x.\,M \rightarrow_{\beta} \lambda x. U \)
the syntax \( [x :=U] \) refers to the lambda terms that results from substituting all occurrences of the unbound variable \( x \) by the term \( U \). This syntax in some sense requires some "work".
There are names given to parts of the above definition:
Redex and contractum
If a subterm of a lambda expression matches the left-hand side of the basis rule above, it is called a redex. This name comes from from reducible expression. The subterm on the right-hand side, \( M[x:=U] \), is called the contractum of the redex.
Multi-step reduction extends the single step relation by augmenting it with reflexivity and transitivity. Before we get to multi-step reduction, we describe the following definition:
Reduction sequence (personal definition)
A reduction sequence is a sequence of lambda terms \( (W_n)_{n=0}^{N} \) such that for every \( n \in \mathbb{N}, \, n \lt N \), we have \( W_n \betaReduction W_{n+1} \). The sequences starts at \( W_0 \) and ends at \( W_N \).
β-reduction, multi-step, \( \twoheadrightarrow_{\beta} \)
Let \( M \) and \( U \) be lambda terms.
\( M \) reduces through multi-step β-reduction to \( U \) iff there exists a reduction sequence starting at \( M \) and ending at \( U \).
Note: the possibility of \( n = 0 \) for multi-step reduction is what introduces the quality of reflexivity to the relation.
For multi-step β-reduction, it is possible for \( M \rightarrow_{\beta} U \) to be true while \( U \rightarrow_{\beta} M \) is false. Below, we extend the multi-step β-reduction with symmetry and arrive at β-equality, an equivalence relation. First, another assisting definition.
Bi-directional reduction sequence (personal definition)
A bi-directional reduction sequence is a sequence of lambda terms \( (W_n)_{n=0}^{N} \) such that for every \( n \in \mathbb{N}, \, n \lt N \) either \( W_n \betaReduction W_{n+1} \) or \( W_{n+1} \betaReduction W_{n} \).
β-equality, \( =_{\beta} \)
Let \( M \) and \( U \) be lambda terms.
\( M \) and \( U \) are said to be β-equal iff there exists a bi-directional reduction sequence starting at \( M \) and ending at \( U \).
β-convertable is sometimes said instead of β-equal.
β-equality extends β-reduction in both directions
If \( M \twoheadrightarrow_{\beta} U \) or \( U \twoheadrightarrow_{\beta} M \) then \( M =_{\beta} U \).
The reverse statement is not true.
Graphs of reduction sequences
The following graph shows a possible reduction sequence that implies that \( W_0 \multiBetaReduction W_3 \) is true. \( W_0 \) multi-step reduces to \( W_0 \), \( W_1 \) and \( W_2 \) also.
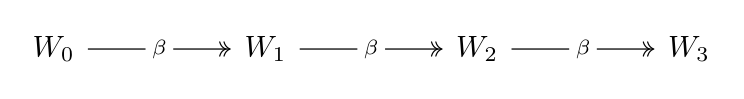
The next graph shows a bi-directional reduction sequence that implies that \( W_0 \betaEq W_5 \) is true. In fact, all nodes are β-equal to each other.

The nodes are in a zig-zag pattern simply to condense the diagram and this layout is not intended to convey any other meaning.
Context
β-reduction → β-normal form → confluence
