Bernoulli Distribution
The bernoulli distribution is a distribution over a single binary random variable.
Suppose you perform an experiment with two possible outcomes: either success or failure. Success happens with probability p, while failure happens with probability 1-p. A random variable that takes value 1 in case of success and 0 in case of failure is called a Bernoulli random variable (alternatively, it is said to have a Bernoulli distribution).
Let  . We say that X has a Bernoulli distribution with parameter p if its probability mass function is:
. We say that X has a Bernoulli distribution with parameter p if its probability mass function is:
 . We say that X has a Bernoulli distribution with parameter p if its probability mass function is:
. We say that X has a Bernoulli distribution with parameter p if its probability mass function is: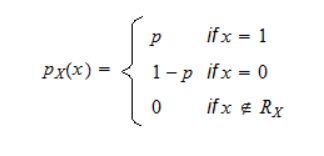
A random variable having a Bernoulli distribution is also called a Bernoulli random variable.
Expected value and variance:
E[X] = p
Var[X] = p(1-p)
A sum of independent Bernoulli random variables is a binomial random variable.
