Entropy

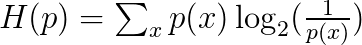
When using variable length encoding to encode a set of tokens, using a shorter code for more common tokens will result in shorter messages on average. The minimum average message length given a distribution of tokens is called the entropy of the distribution.
Codespace and decodability
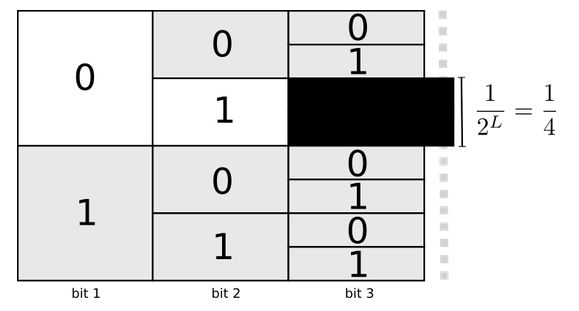
When designing variable length coding schemes, codes must be designed to be uniquely decodable. For example, if 0 and 01 are both codewords, then it is not clear which code begins the string: 0100111 [or is it?]. One way of making codes uniquely decodable is to assert that no codeword should be the prefix of another codeword. Codes that obey this rule are called prefix codes.
One way to think about this is that every codeword requires a sacrifice from the space of possible codewords. If we take the codeword 01, we lose the ability to use any codewords it's a prefix of. The space lost by using the codeword 01, of length 2, is a quarter of all possible codewords:

Optimum encodings
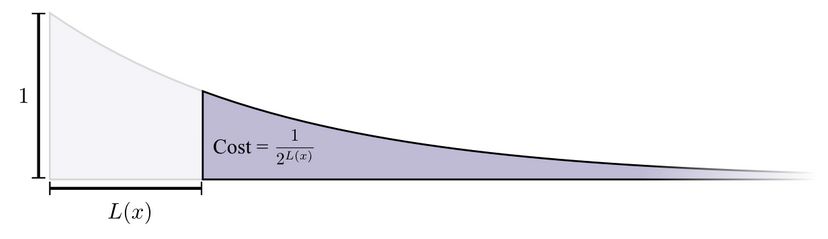
You can think of having a limited budget to spend on getting short codewords. We pay for one codeword by sacrificing a fraction of possible codewords. Short codewords reduce the average message length be are expensive in using up the available codewords.
The cost of codewords decreases exponentially with the length of the codeword:
(Shown here with natuaral logarithm, instead of base 2. A constant factor can express the difference).

Note that if the cost decays as a (natural) exponential, it is both the height and the area.
A way of arriving at an optimum encoding is to distribute our budget in proportion to how common an event is. So if one event happens 50% of the time, we spend 50% of our budget buying a short codeword for it.
From the decaying exponential above, and the assertion that we will spend p(x) on a codeword for event x, we can state the following:

After choosing the codeword length for each word, we can calculate the fundamental limit of how short one can get the average message to communicate events from a particular probability distribution, p. This limit, the average message length using the best possible code, is called the entropy of p, H(p). This average message length is the expected message length:
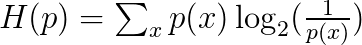
Implications
This average amount of information needed to communicate something has clear implications for compression. It also quantifies uncertainty: If I knew for sure what was going to happen, I wouldn't have to send a message at all; if there's 64 different things that could happen with 50% probability, I need to send 6 bits. The more concentrated the probability, the shorter the average message that can be cleverely crafted. The more uncertain the outcome, the more I learn, on average, when I find out what happened.
Copied from:
http://colah.github.io/posts/2015-09-Visual-Information/#fnref1
Example
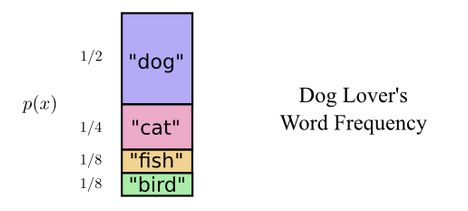
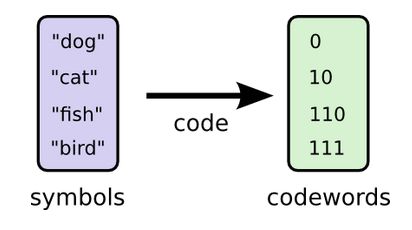
Given the messages and frequencies:

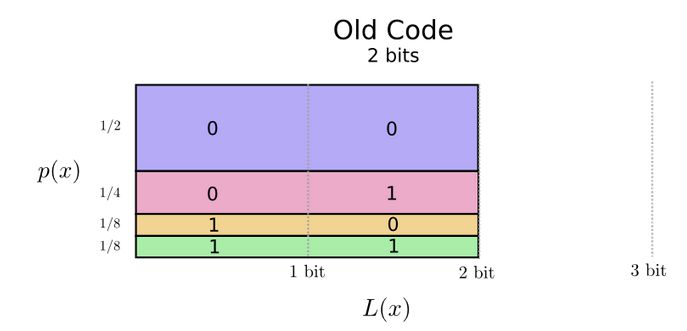
One possible encoding is a fixed length encoding:

L(x) is the length of the codeword; p(x) is the probability of each word being sent.
In this case, the average encoding length is 2 bits.
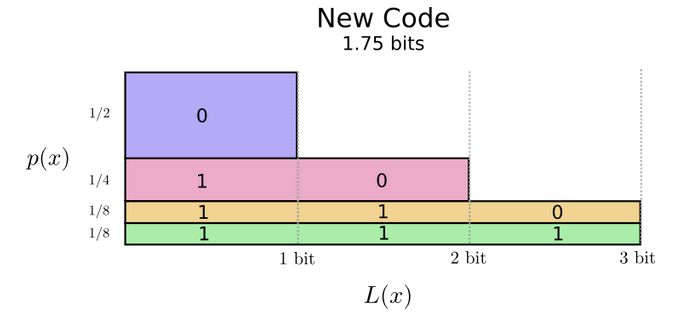
Another possible encoding uses a short codeword for the most common words:

The codeword length chart looks like:

The average encoding length is now a shorted 1.75 bits, the fundamental limit for this distribution. Thus, it is said that the entropy of the distribution = the area of the bars = 1.75 bits.
