\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Question
Incremental average (estimate update)

Statement:

\begin{displaymath} A_n = A_{n-1} + \frac{1}{n}(V_n - A_{n-1}) \end{displaymath}

Alterative form:

\begin{displaymath}NewEstimate \leftarrow OldEstimate + StepSize[NewData - OldEstimate]\end{displaymath}

The second form describes updating our estimate of the average by multiplying an error term, NewData - OldEstimate, by a weighting factor, StepSize. StepSize is $\frac{1}{n}$ when all data points are weighted equally. 

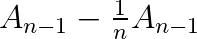The average, $A_{n-1}$ is known for a sequence of n-1 values, $V_1, V_2, ..., V_{n-1}$. If the next value, $V_n$ is included in the sequence, the new average, $A_{n}$, can be computed by adding the new component of the average, $\frac{1}{n}V_{n}$, to the old average transfered from an $n-1$ denominator to an $n$ denominator, ($A_{n-1} - \frac{1}{n}A_{n-1}$). 

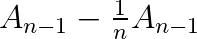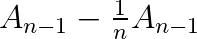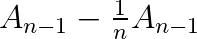The ($A_{n-1} - \frac{1}{n}A_{n-1}$) component is easy to understand from an example: the difference between 1/4 and 1/5 is 1/(4*5). If we want to find the total divided by 5, and already have the total divided by 4, we can obtain the former by subtracting the known difference, 1/(4*5), which is the average divided by 4, divided by 5 again.