What is the derivative of negative log MLE (MLE used as a negative cost) when the variables are passed through softmax activations?
The derivative of the cost function is needed for
back-propagation.
When the output layer uses a MLE/cross-entropy cost and softmax activation,
the derivative of the cost function combined with the activation function
simplifies to a very simple expression. This note covers this
computation.
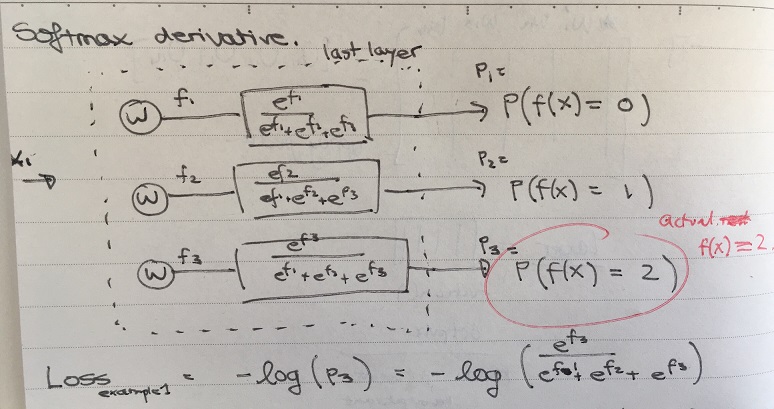
Consider the last layer of a neural network shown below:
For the given training example \( x_1 \), the correct category is 2 (out of
all categories 0,1 and 2). Only the output corresponding to category 2 is used
in the calculation of the loss contributed by the example. The loss is given
by:
\[ Loss_{ex_1} = -ln(p_3) = -ln(\frac{e^{f_3}}{e^{f_1} + e^{f_2} + e^{f_3}}) \]
While only the probability for the correct category is used to calculate
the loss for the example, the other outputs, \( p_1 \) and \( p_2 \) still
affect the loss, as \( p_3 \) depends on these values (all sum to 1).
The partial derivatives will be:
\[
\begin{align*}
\frac{\partial L}{\partial f_1} &= p_1 \\
\frac{\partial L}{\partial f_2} &= p_2 \\
\frac{\partial L}{\partial f_3} &= -(1-p_3) = p_3 - 1\end{align*}
\]
So if we have output probabilities [0.1, 0.3, 0.6], then the derivative of
the loss with respect to last layer's output before applying the softmax
activation will be [0.1, 0.3, -0.4].
Derivations
Formulating the derivative of loss wrt different variables is simplified if
the log and exponential are canceled at the beginning:
\[
\begin{align*}
Loss_{ex_1} = -ln(p_3) &= -ln(\frac{e^{f_3}}{e^{f_1} + e^{f_2} + e^{f_3}}) \\
&= ln(\frac{e^{f_1} + e^{f_2} + e^{f_3}}{e^{f_3}}) \\
&= ln(e^{f_1} + e^{f_2} + e^{f_3}) - ln(e^{f_3}) \\
&= ln(e^{f_1} + e^{f_2} + e^{f_3}) - f_3 \end{align*}
\]
From here, the partial derivates are obvious. For example:
\[
\begin{align*}
\frac{\partial L}{\partial f_1} &= \frac{\partial}{\partial f_1}(ln(e^{f_1} + e^{f_2} + e^{f_3}) - f_3) \\
&= \frac{\partial}{\partial x}(ln(x)) \frac{\partial}{\partial f_1}(e^{f_1} + e^{f_2} + e^{f_3}) \\
&= \frac{1}{x} e^{f_1} \\
&= \frac{e^{f_1}}{e^{f_1} + e^{f_2} + e^{f_3}} \\
&= p_1
\end{align*}
\]
The below image is part of a separate card, but I'm including it here, as it is quite
relevant.

Old image:
Some old stuff:
Given the loss (lets just call it L, with the example 1 being implicit), we
wish to find: 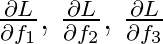 . First consider
. First consider
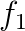 :
:
\[
\begin{align*}
\frac{\partial L}{\partial f_1} = \frac{\partial}{\partial f_1}(-ln(p_3)) &= (\frac{\partial}{\partial x}(-ln(x)) (\frac{\partial}{\partial y}(\frac{e^{f_3}}{y + e^{f_2} + e^{f_3}}))(\frac{\partial}{\partial f_1}(e^{f_1})) \\
\text{where } x = \frac{e^{f_3}}{y + e^{f_2} + e^{f_3}}, \text{ and } y = e^{f_1} \\
&= (- \frac{1}{x})(\frac{-e^{f_3}}{(y + e^{f_2} + e^{f_3})^2})(e^{f_1}) \\
&= (-\frac{e^{f_1} + e^{f_2} + e^{f_3}}{e^{f_3}})(\frac{-e^{f_3}}{(e^{f_1} + e^{f_2} + e^{f_3})^2})(e^{f_1}) \\
&= \frac{e^{f_1}}{e^{f_1} + e^{f_2} + e^{f_3}} \\
&= p_1
\end{align*}
\]
Similarly,  .
. 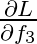 is calculated as follows:
is calculated as follows:
\[
\begin{align*}
\frac{\partial L}{\partial f_3} = \frac{\partial}{\partial f_3}(-ln(p_3)) &= (\frac{\partial}{\partial x}(-ln(x)) (\frac{\partial}{\partial y}(\frac{e^{f_3}}{e^{f_1}+ e^{f_2} + y}))(\frac{\partial}{\partial f_3}(e^{f_3})) \\
\text{where } x = \frac{e^{f_3}}{e^{f_1} + e^{f_2} + y}, \text{ and } y = e^{f_3} \\
&= (- \frac{1}{x})(\frac{1}{e^{f_1} + e^{f_2} + y} - \frac{e^{f_3}}{e^{f_1} + e^{f_2} + y})(e^{f_3}) \\
&= (- \frac{e^{f_1} + e^{f_2} + e^{f_3}}{e^{f_3}})(\frac{1}{e^{f_1} + e^{f_2} + e^{f_3}} - \frac{e^{f_3}}{e^{f_1} + e^{f_2} + e^{f_3}})(e^{f_3}) \\
&= -(1 - \frac{e^{f_3}}{e^{f_1} + e^{f_2} + e^{f_3}}) \\
&= p_3 - 1
\end{align*}
\]




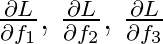 . First consider
. First consider
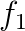 :
: .
. 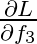 is calculated as follows:
is calculated as follows: