Math and science::INF ML AI
Entropy of an ensemble
The entropy of an ensemble, \( X = (x, A_x, P_x) \), is defined to be the average Shannon information content over all outcomes:
\[ H(X) = \sum_{x \in A_x}P(x) \log \frac{1}{P(x)} \]
Properties of entropy:
- \( H(X) \geq 0 \) with equality iff some outcome has probability 1.
- Entropy is maximized if the probability of outcomes is uniform.
- The Entropy is less than the log of the number of outcomes.
The last two points can be expressed as:
\[H(X) \leq \log(|A_x|) \text{, with equality iff all outcomes have probability } \frac{1}{|A_x|} \]
Proof on the back side.
Proof that \( H(X) \leq \log(|A_x|) \):
First note that:
\[
\begin{align*}
E[\frac{1}{P(X)}] &= \sum_{i \in A_x} P(i) \frac{1}{P(i)} \\
&= \sum_{i \in A_x} 1 \\
&= |A_x| \\
\end{align*}
\]
Now then:
\[
\begin{align*}
H(X) &= \sum_{i \in A_x} P(i) \log\frac{1}{P(i)} \\
&= \sum_{i \in A_x}P(i)f(\frac{1}{P(i)}) \\
\end{align*}
\]
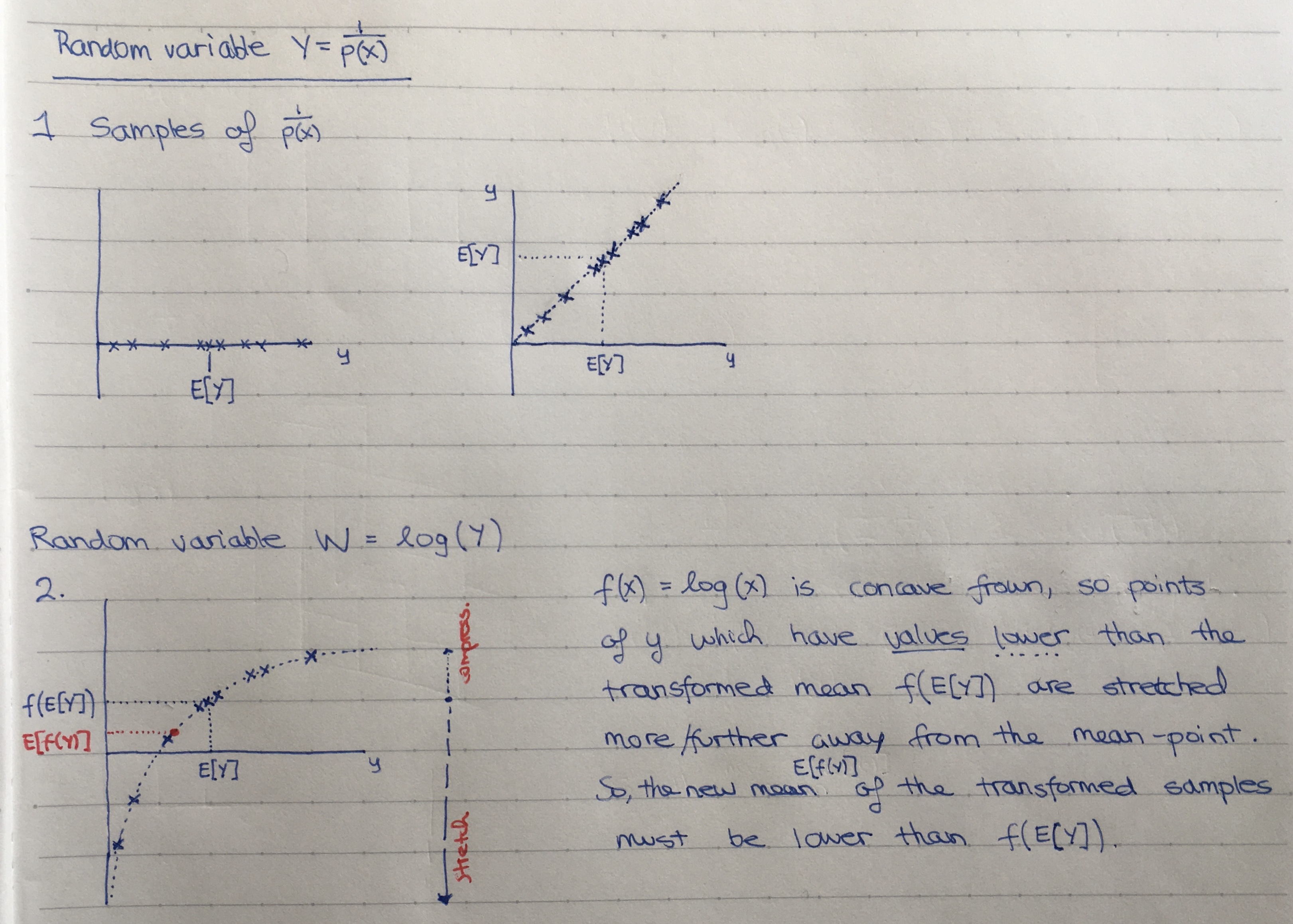
Where \( f(u) = \log(u) \) is a concave function. Then, Using Jensen's inequality we can say:
\[
\begin{align*}
H(X) &= E[f(\frac{1}{P(X)})] \\
&\leq f(E[\frac{1}{P(X)}]) \\
&= \log(|A_x|)
\end{align*}
\]

Perspectives on entropy:
- If \( X \) is a random variable, we can create another random variable, let's call it \( Y \), by applying a fuction to the outcomes, \( Y = f(X) \). What if this function depended not on the value of the outcome, but on the probability of the outcome? As there is a function P that maps outcomes to probabilities, we could create a random variable \( Y = P(X) \). For Shannon information content and entropy, we create the variable \( Y = \log \frac{1}{P(X)} \). The entropy is the expected value of this random variable.
