Jensen's inequality
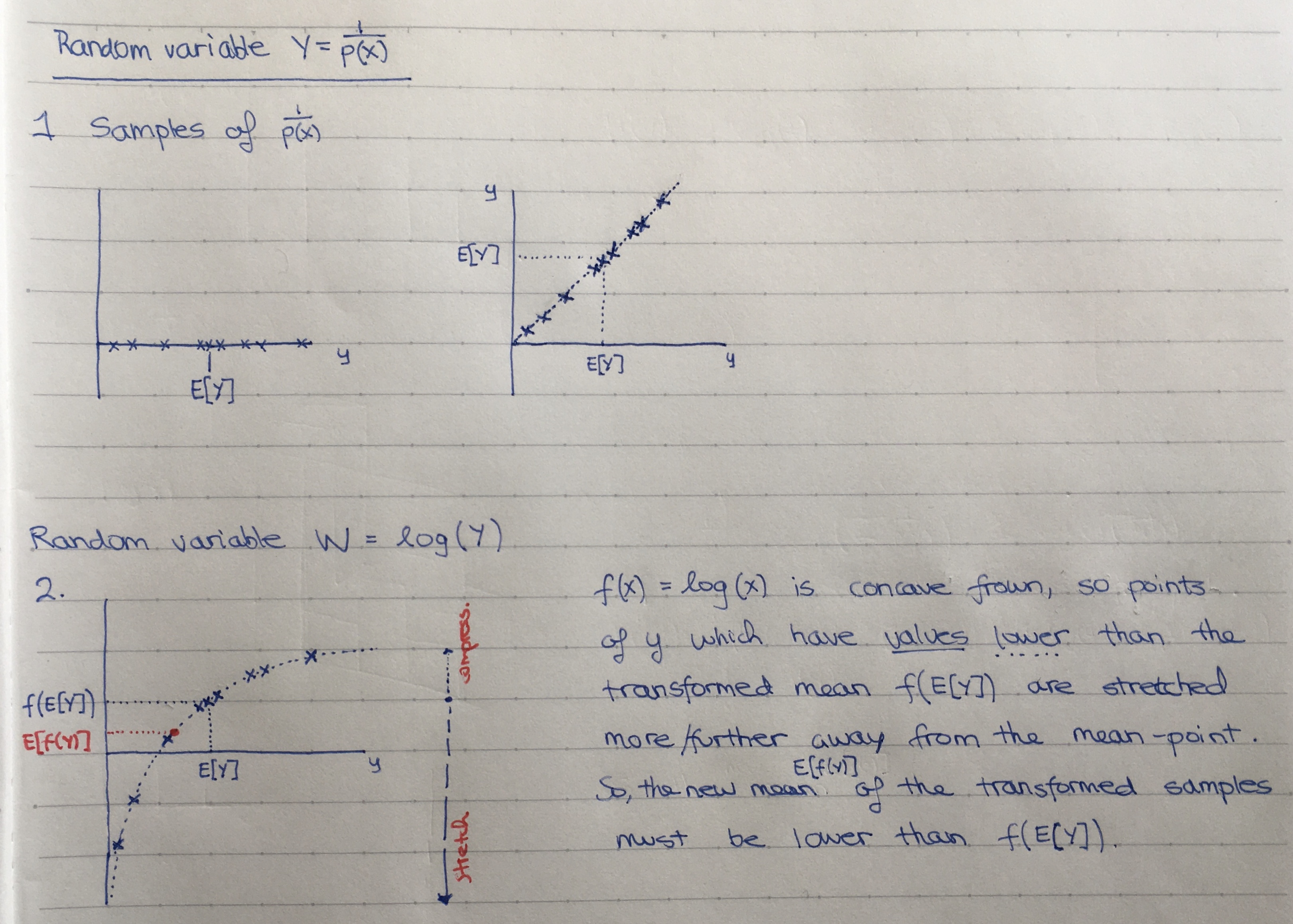
If \( f \) is a convex (smile) function and \( X \) is a random variable then:
\[ E[f(X)] \ge f(E[X]) \]
If \( f \) is strictly convex and \( E[f(X)] = f(E[X]) \), then the random variable \( X \) is a constant.
Intuition:

Proof:
Intuition #2
The following is taken from Andrew Ng's notes for CS229: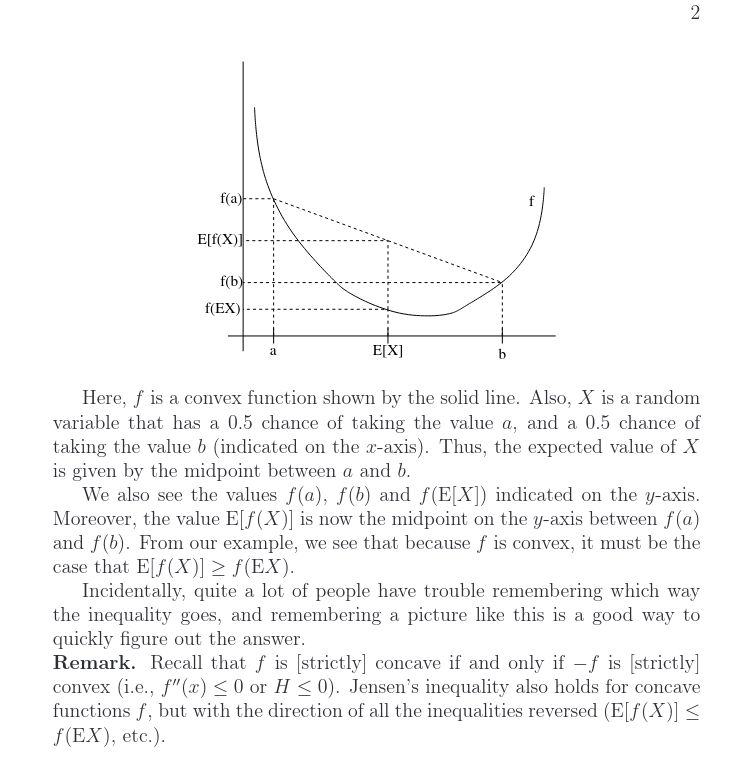
TODO
Example
Q1: Three squares
Three squares have average area \( \bar{A} = 100 m^2 \). The average of the lengths of their sides is \( \bar{l} = 10 m \). What can be said about the size of the largest of the three squares?
A1:
Let \( x \) be the length of the side of a square, and let the probability of \( x \) be \( \frac{1}{3}, \frac{1}{3}, \frac{1}{3} \) over the three lengths, \( l_1, l_2, l_3 \). Then the information that we have is:
* \( E[X] = 10 \)
* \( E[f(X)] = 100 \text{, where } f(x) = x^2 \)
\( f \) is a strictly convex function and the equality \( E[f(X)] = f(E[X]) \) holds, so by Jensen's equality, \( x \) must be a constant and all three lengths must be equal. So the area of the largest square (and all squares) is \(100 m^2 \).
