Motivating the logistic and softmax output layers through a great exercise.



p(x_1, ..., x_n) &= p(x_1 \vert x_2, ..., x_n)p(x_2, ..., x_n) \\
&= p(x_1 \vert x_2, ..., x_n)p(x_2 \vert x_3, ..., x_n)p(x_3, ..., x_n) \\
&= p(x_n) \prod_{i=1}^{n-1} {{c1::p(x_i \vert x_{i+1}, ..., x_n)}}
\end{aligned}
\]
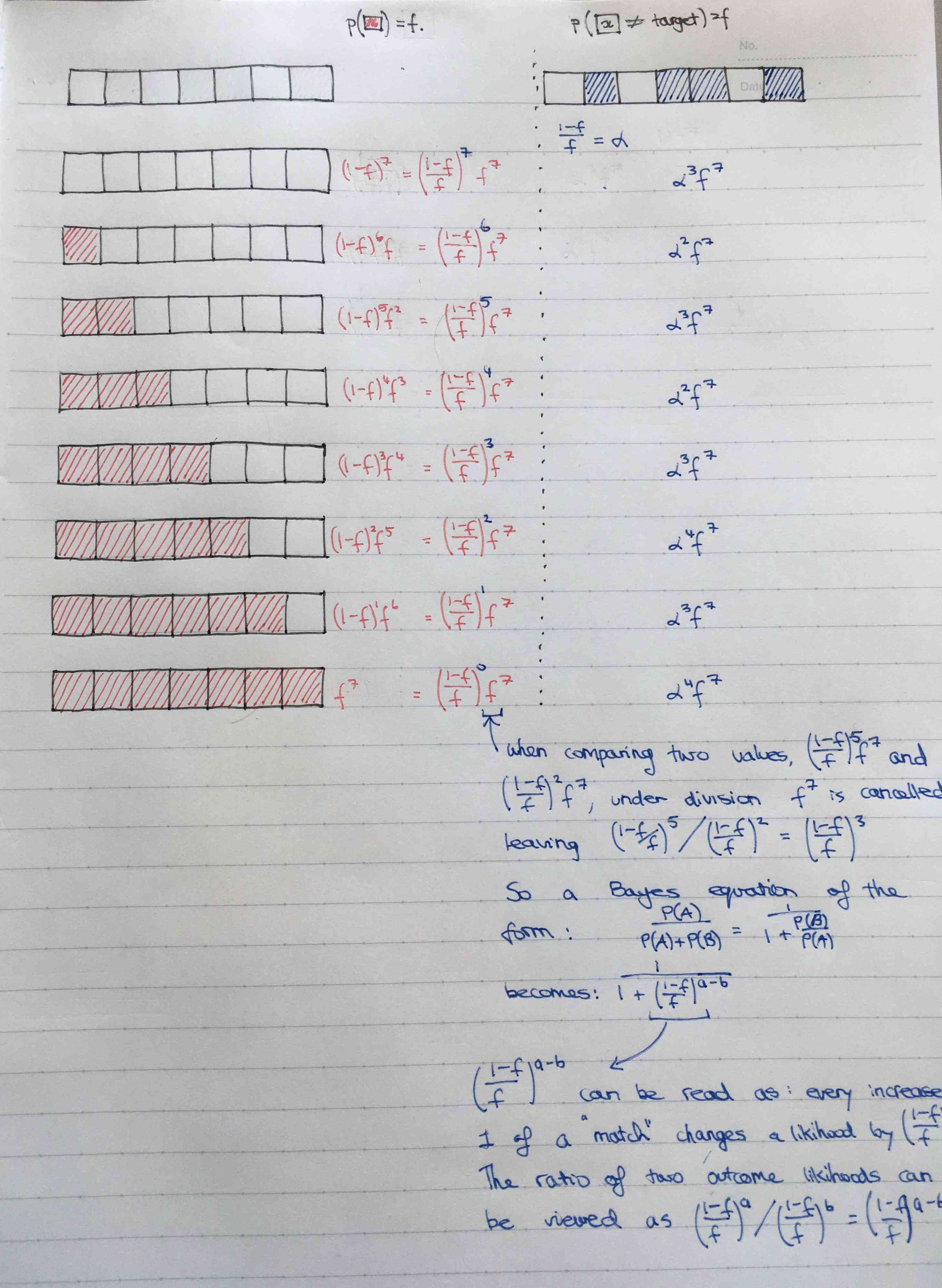
The basic idea is that Bayes's rule can be mutated as follows:
\begin{aligned}
P(s=2|x=x)&= \frac{P(x|s=2)P(s=2)}{\sum_{i \in \{2, 3\}} P(x | s = i)P(s = i) } \\
&= \frac{P(x|s = 2)P(s=2)}{P(x | s = 2)P(s = 2) + P(x | x = 3)P(s = 3) } \\
&= \frac{1+\frac{P(x|s=3)P(s = 3)}{P(x|s=2)}} \\
\end{aligned}
\]
an represent \( P(x = x_1 | s_2) \) as a function of the dot product of two vectors, for example:
Let
\( x_1 = \begin{bmatrix}1 & -1 & -1 & -1 & -1 & -1 & -1 \end{bmatrix} \),
which repesents the LED set with only the 1st LED on and we define the vector
\( s_2 = \begin{bmatrix}1 & -1 & 1 & 1 & 1 & 1 & -1\end{bmatrix} \),
then \( x_1 s_2 \) can be related to the number of correct digits like so:
\( C = correctCount = \frac{x_1 s_2 + 7}{2} \)
P(s=2|x=x)&=\frac{P(x|s=2)P(s=2)}{\sum_{i \in \{2, 3\}} P(x | s = i)P(s = i) } \\
&=\frac | s = 2)P(s=2)}{P(x | s = 2)P(s = 2) + P(x | x = 3)P(s = 3) } \\
=&\frac1+\frac{P(x|s=3)P(s = 3)}{P(x|s=2)})} \\
\end{aligned}
\]
Thus we see how the probability can be molded into an exponential form, and how Bayes's rule allows for the \( \frac{1}{1 + e^{f(x)}} \) form. With more than two classes, it's easier to express the probability without dividing the numerator and denomitator by the numerator, so we are left with the softmax form as show in the question. Thus, it is easy to see how the softmax and the logistic output units are essentially the same thing: relative probabilities when expresses as exponentials.
A generality
If a random variable has two possible values and you can express the event probabilities as \( \alpha^{-x_1} \) and \( \alpha^{-x_2} \), then you can arrive at an exponential formulation like so:
\[ \frac{\alpha^{-x_1}}{\alpha^{-x_1} + \alpha^{-x_2}} = \frac{1}{1 + \alpha^{-(x_2 - x_1)}} = \frac{1}{1 + e^{-\beta x}} \] Where \(x = x_2 - x_1 \).