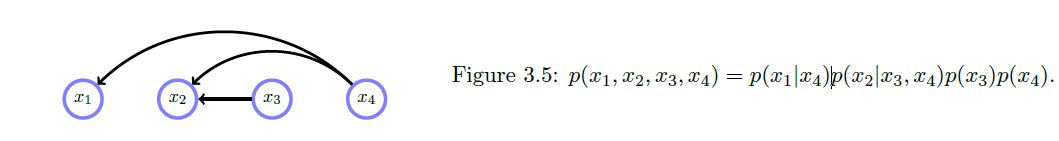Belief networks
A belief network (called a Bayesian network by Koller) is a grapical model that represents a distribution of the formParental variables is just a term for the variables that appear as conditional variables for a given variable.
A belief network represents a distribution as a directed graph where the \( i \)th node corresponds to the factor \( p(x_i \vert pa(x_i)) \), with directed connections from all \( pa(x_i) \) nodes to the \( i \)th node.
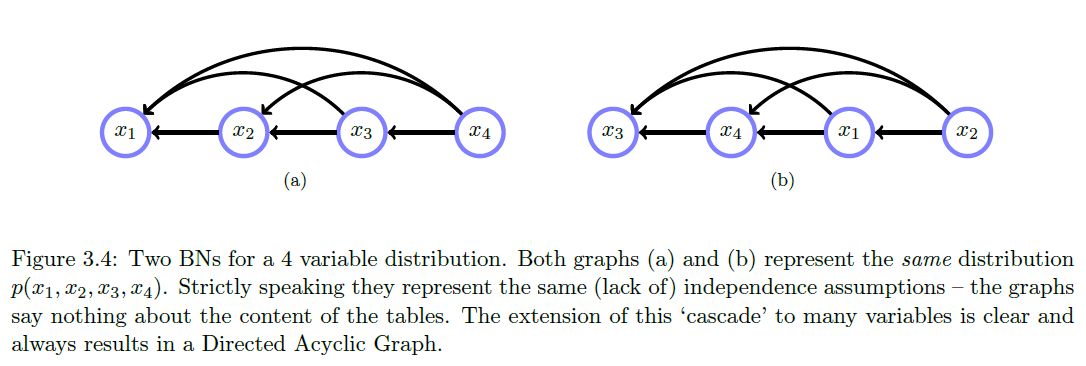
According to the rules above, a distribution \( p(x_1, x_2, x_3, x_4) \), one with no independence statements, can be modelled with a cascade graph like so:
Derivation
Without loss of generality, using Bayes' rule the distribution \( p(x_1, ..., x_n) \) can be represented as:
\[
\begin{aligned}
p(x_1, ..., x_n) &= p(x_1 \vert x_2, ..., x_n)p(x_2, ..., x_n) \\
&= p(x_1 \vert x_2, ..., x_n)p(x_2 \vert x_3, ..., x_n)p(x_3, ..., x_n) \\
&= p(x_n) \prod_{i=1}^{n-1} p(x_i \vert x_{i+1}, ..., x_n)
\end{aligned}
\]
More accurately, a belief network represents a set of distributions that have the same dependency relationships, not just a single distribution with speficied probabilities.
Example
Deleting any connection represents the existance of some independence. For example: