Math and science::INF ML AI
Belief networks: independence
It's not immediately obvious how to interpret the conditional relationships represented by a belief network. For example, consider the networks below. 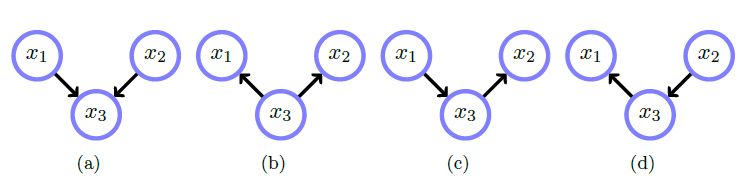
Network(s) [...] represent the distribution:
\[\begin{aligned}p(x_1, x_2, x_3) &= p(x_1 \vert x_3)p(x_2 \vert x_3)p(x_3) \\&= p(x_2 \vert x_3)p(x_3 \vert x_1)p(x_1) \\&= p(x_1 \vert x_3)p(x_3 \vert x_2)p(x_2) \end{aligned} \]
Network(s) [...] represent the distribution:
\[ p(x_1, x_2, x_3) = p(x_3 \vert x_1, x_2)p(x_1)p(x_2)\]
Next, consider conditional independence.
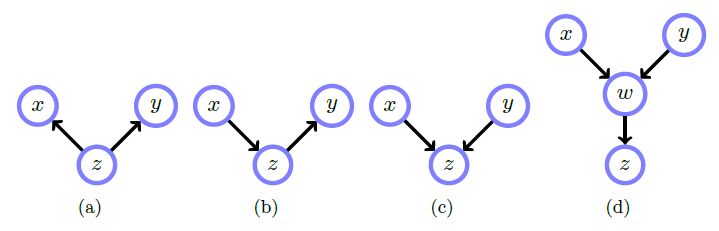
- In a), \( x \) and \( y \) are unconditionally dependent, and conditioned on \( z \) they are independent. Knowing either gives information on the distribution of \( z \), which in turn informs of the others distribution.. \( p(x, y \vert z) = p(x \vert z)p(y \vert z) \)
- In b), \( x \) and \( y \) are unconditionally dependent, and conditioned on \( z \) they are independent. \( p(x, y \vert z) \varpropto p(z \vert x)p(x)p(y \vert z) \)
- In c), \( x \) and \( y \) are unconditionally independent, and conditioned on \( z \) they are dependent. \( p(x, y \vert z) \varpropto p(z \vert x, y)p(x)p(y) \)
- Id d), \( x \) and \( y \) are unconditionally independent, and conditioned on \( z \) or \( w \), are dependent. See book for full equation.
