Math and science::INF ML AI

Belief networks: independence

It's not immediately obvious how to interpret the conditional relationships represented by a belief network. For example, consider the networks below.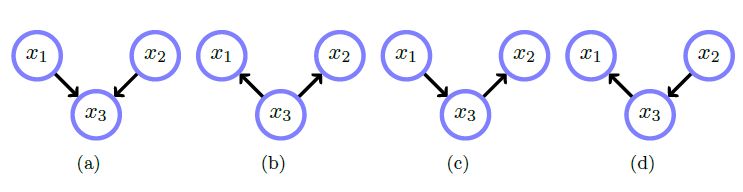

Network(s) b, c and d represent the distribution:

\begin{aligned} p (x_{1}, x_{2}, x_{3}) & = p (x_{1} | x_{3}) p (x_{2} | x_{3}) p (x_{3}) \\ = p (x_{2} | x_{3}) p (x_{3} | x_{1}) p (x_{1}) \\ = p (x_{1} | x_{3}) p (x_{3} | x_{2}) p (x_{2}) \end{aligned}

Network(s) a represent the distribution:

p (x_{1}, x_{2}, x_{3}) = p (x_{3} | x_{1}, x_{2}) p (x_{1}) p (x_{2})

Next, consider conditional independence.

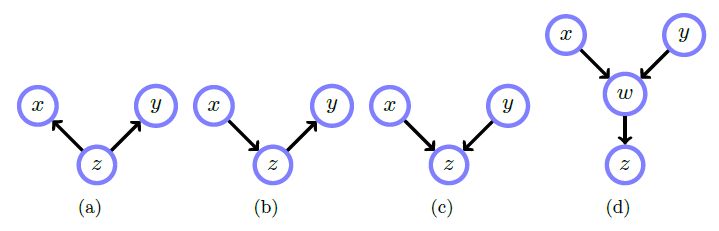
In a), $x$ and $y$ are unconditionally dependent, and conditioned on $z$ they are independent. Knowing either gives information on the distribution of $z$ , which in turn informs of the others distribution.. $p (x, y | z) = p (x | z) p (y | z)$
In b), $x$ and $y$ are unconditionally dependent, and conditioned on $z$ they are independent. $p (x, y | z) \propto p (z | x) p (x) p (y | z)$
In c), $x$ and $y$ are unconditionally independent, and conditioned on $z$ they are dependent. $p (x, y | z) \propto p (z | x, y) p (x) p (y)$
Id d), $x$ and $y$ are unconditionally independent, and conditioned on $z$ or $w$ , are dependent. See book for full equation.

Independent but conditionally dependent

Considering a graph like $A \to B \leftarrow C$ , we have $A$ and $C$ being (unconditionally) independent. However, conditioning on $B$ makes them dependent. Intuitively, whilst we believe the root causes are independent, given the value of the observation, we learn something about the state of both the causes. Another way of viewing this is: the outcome $B$ requires knowledge of both $A$ and $C$ before we have an independent distribution. Thus, if we know $B$ , then the dependecy of $B$ on $C$ will change depending on the value of $A$ . Thus, if $B$ is known, $C$ is dependent on $A$ .

Tips

So far, the most intuitive way I have found of converting these diagrams into a mental model is to view the arrows into a node A as saying: knowing the inputs to A is sufficient to fix the shape of A's distribution, and all other quantities can change without affecting A's distribution.

When reading the graphs, have the following rules in mind:

source exists in the conditional of target when expressing $p (x_{1}, . . ., x_{n})$
When expressing $p (x_{1}, . . ., x_{n})$ as $p (x_{t} | d e p e n d e n c i e s) p (d e p e n d e n c i e s)$ , it can be done as $p (x_{t} | i n p u t s, o u t p u t s) p (i n p u t s, o u t p u t s) p (o t h e r)$ . Where $p (o t h e r)$ accounts for any other connected components in the full graph. (I'm not sure if I have this right).

Source

Bayesian Reasoning and Machine Learning

David Barber

p40-41

14.11.2019