\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
Math and science::INF ML AI

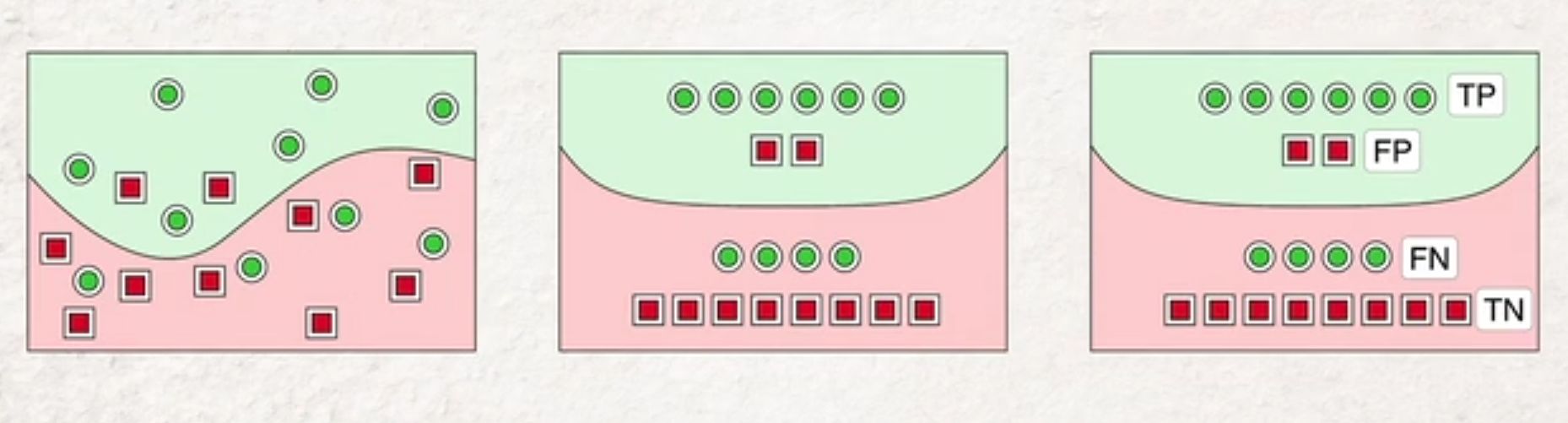
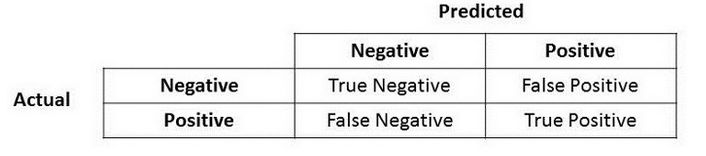
Accuracy, precision, recall


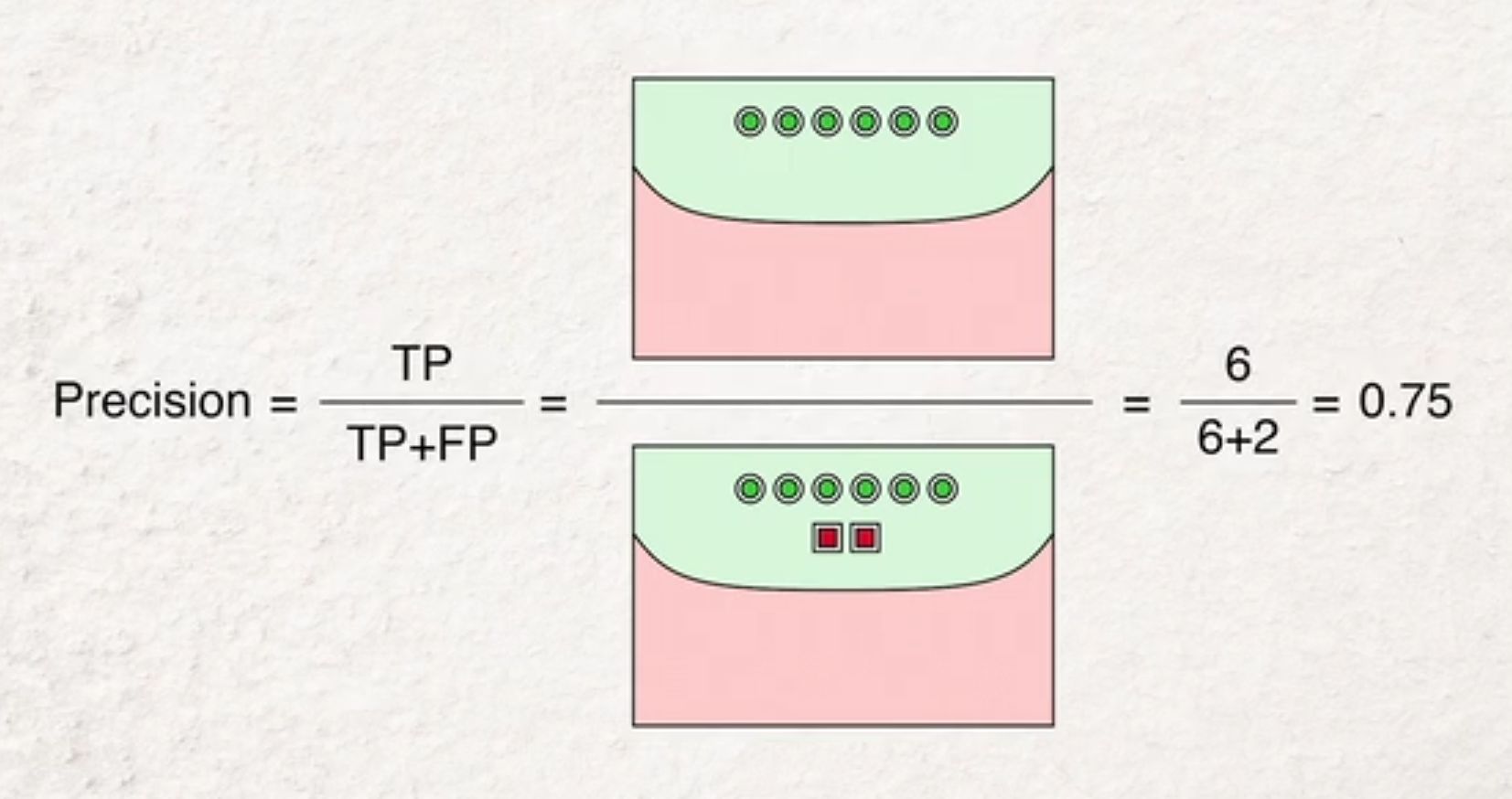
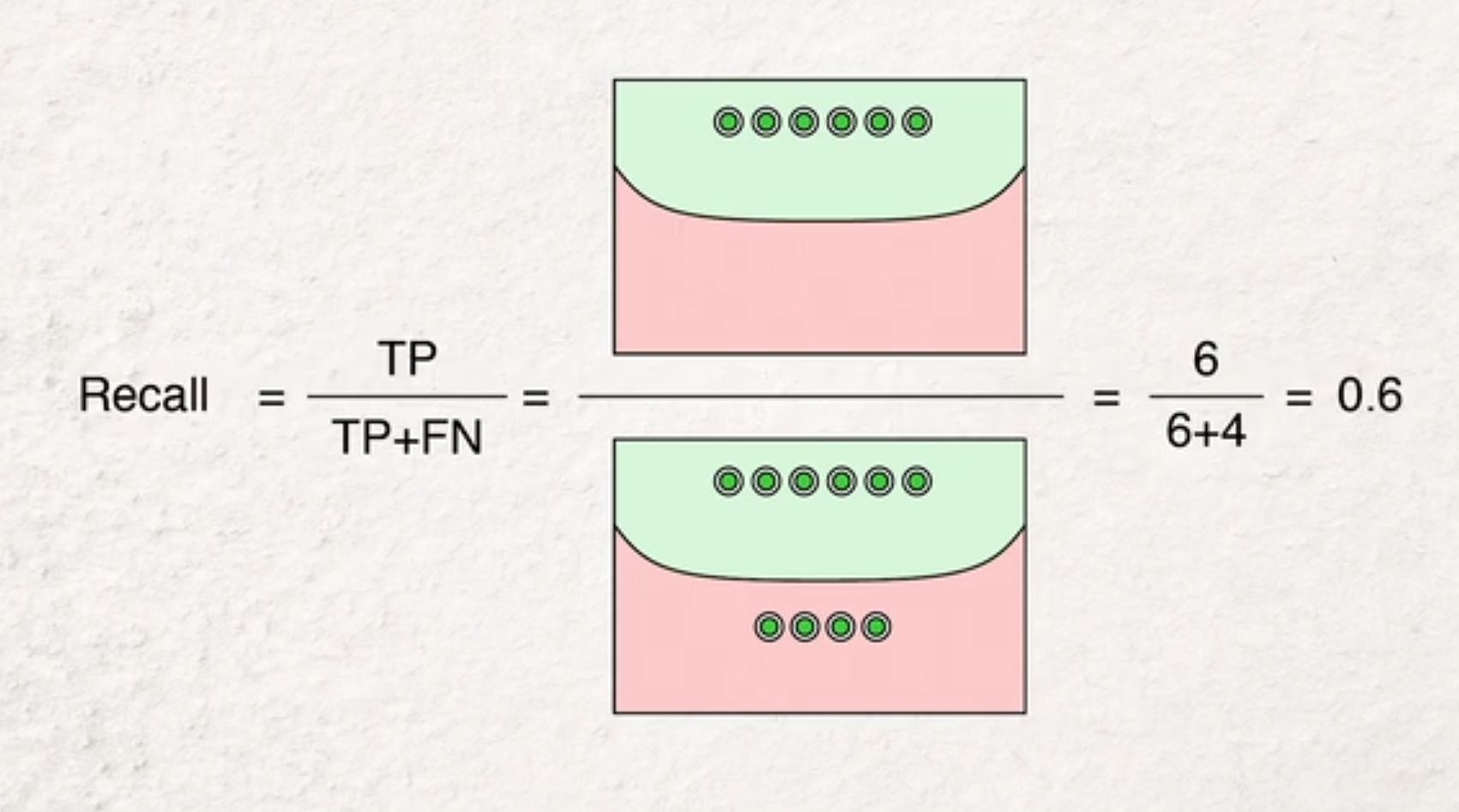
\[ \begin{aligned} \text{accuracy} &= \frac{TP + TN}{TP + TN + FP + FN} \\ \text{precision} &= \frac{TP}{TP + FP} \\ \text{recall} &= \frac{TP}{TP + FN} \\ \end{aligned} \]

Formulated in words

accuracy = \( \frac{ \text{correct} }{ \text{incorrect} } \)

precision = given a positive result, how likely is the true state to be positive; the reliability of a positive result.

recall = how many of the true positives are recoreded as positive. Have we missed many positives?

Pathalogical and benign examples

Are false positives dangerous? Are false negatives dangerous? Poor precision affords many false positives. Poor recall affords many false negatives. If the true/false meaning of any test is reversed, false positives become false negatives and vice versa.

  • Poor precision is pathalogical: COVID19 testing where positive represents being free of the virus.
  • Poor precision is benign: COVID19 testing, where a positive represents having the virus.
  • Poor recall is pathalogical: COVID19 testing, where a positive represents having the virus.
  • Poor recall is benign: COVID19 testing where positive represents being free of the virus.