\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Answer
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
Math and science::INF ML AI

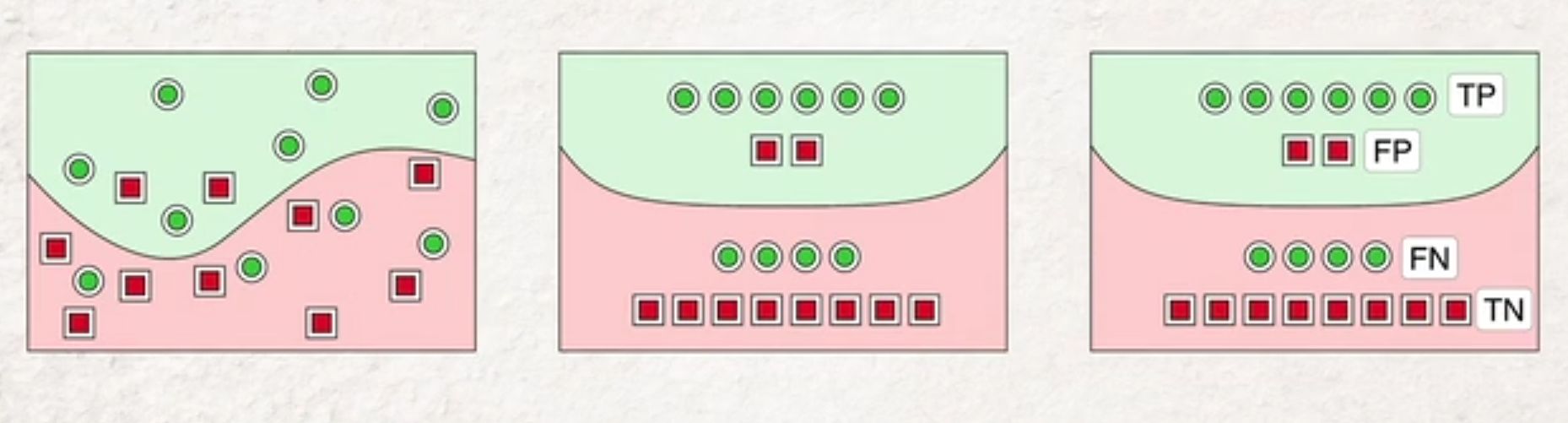
Accuracy, precision, recall


[\[ \begin{aligned} \text{accuracy} &= \frac{?}{?} \\ \text{precision} &= \frac{?}{?} \\ \text{recall} &= \frac{?}{?} \\ \end{aligned} \] ]

Formulated in words

accuracy = [\( \frac{ \text{something} }{ \text{something} } \) ]

precision = [...]

recall = [...]

Pathalogical and benign examples

Are false positives dangerous? Are false negatives dangerous? Poor precision affords many false positives. Poor recall affords many false negatives. If the true/false meaning of any test is reversed, false positives become false negatives and vice versa.

  • Poor precision is pathalogical: COVID19 testing where positive represents [having/being free of the virus?].
  • Poor precision is benign: COVID19 testing, where a positive represents [having/being free of the virus?].
  • Poor recall is pathalogical: COVID19 testing, where a positive represents [having/being free of the virus?].
  • Poor recall is benign: COVID19 testing where positive represents [having/being free of the virus?].