\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
Math and science::Topology

Metric space. ε-balls

Let \( X \) be a metric space, let \( x \in X \) and let \( \varepsilon > 0 \) be a real. The open ε-ball around \( x \) (or in more detail, the open ball around \( x \) of radius \( \varepsilon \)) is the subset of \( X \) given by

\(B(x, \varepsilon) = \{y \in X : d(x, y) < \varepsilon \} \)

Similarly, the closed ε-ball around \( x \) is

\(\bar{B}(x, \varepsilon) = \{y \in X : d(x, y) \le \varepsilon \} \)

The definition of open sets in metric spaces is formulated in terms of open ε-balls.

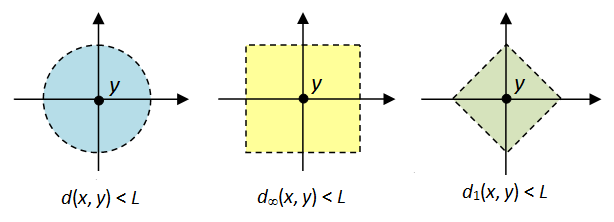
Example

Metrics such as \( d_1 \), \( d_2 \) and \( d_\infty \) for both \( \mathbb{R}^n \) and continuous function spaces \( C[a, b] \), and other metrics such as Hamming distance, each induce ε-balls within the space they are applied in. It is interesting to consider what the ε-ball in each metric space is.


Context