\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
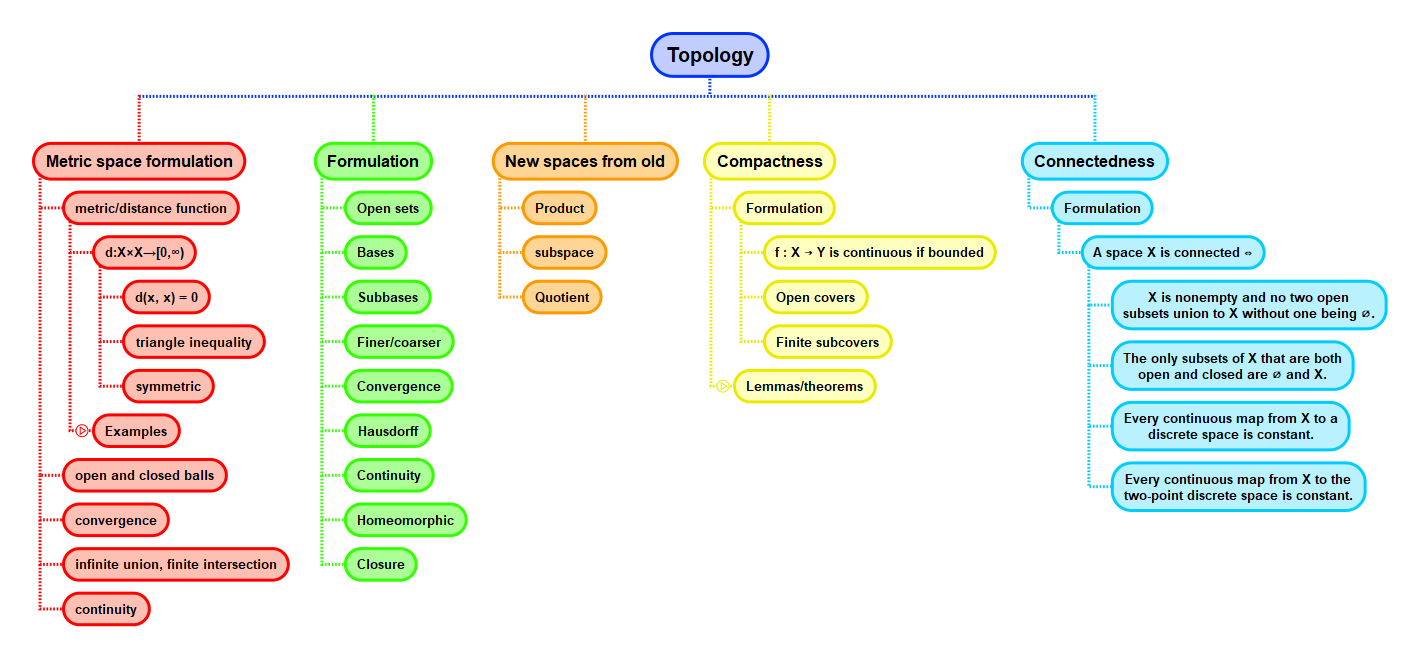
Math and science::Topology

Metric space. Open and closed sets

Open and closed subsets

Let \( X \) be a metric space.

Open in \( X \)
A subset \( U \) of \( X \) is open in \( X \) iff for all \( u \in U \), there exists an \( \varepsilon > 0 \) such that \( B(u, \varepsilon) \subseteq U \).
Closed in \( X \)
A subset \( V \) of \( X \) is closed in \( X \) iff \( X \setminus V \) is open in \( X \).

Tom Leinster describes the openness of \( U \):

Thus, \( U \) is open if every point of \( U \) has some elbow room—it can move a little bit in each direction without leaving \( U \).

Personally, I like the phrase: every element of an open set has a neighbourhood.

ε-balls

Open ε-balls are open, and closed ε-balls are closed. Consider trying to prove this. They are open on account of the definition of openness, not by their own definition alone, despite their names being suggestive.


Open, closed, neither or both

Subsets of a metric space can be any combination of open and closed.


Open subset, closed subset

There's no such thing as an open set that is not an open subset; \( U \) is open in \( X \). The importance of this is that a set \( U \) may be open in one space and not open in another. \( [0, 1) \) is not open in \( \mathbb{R} \) but is open in \( [0, 2] \).

Context