\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
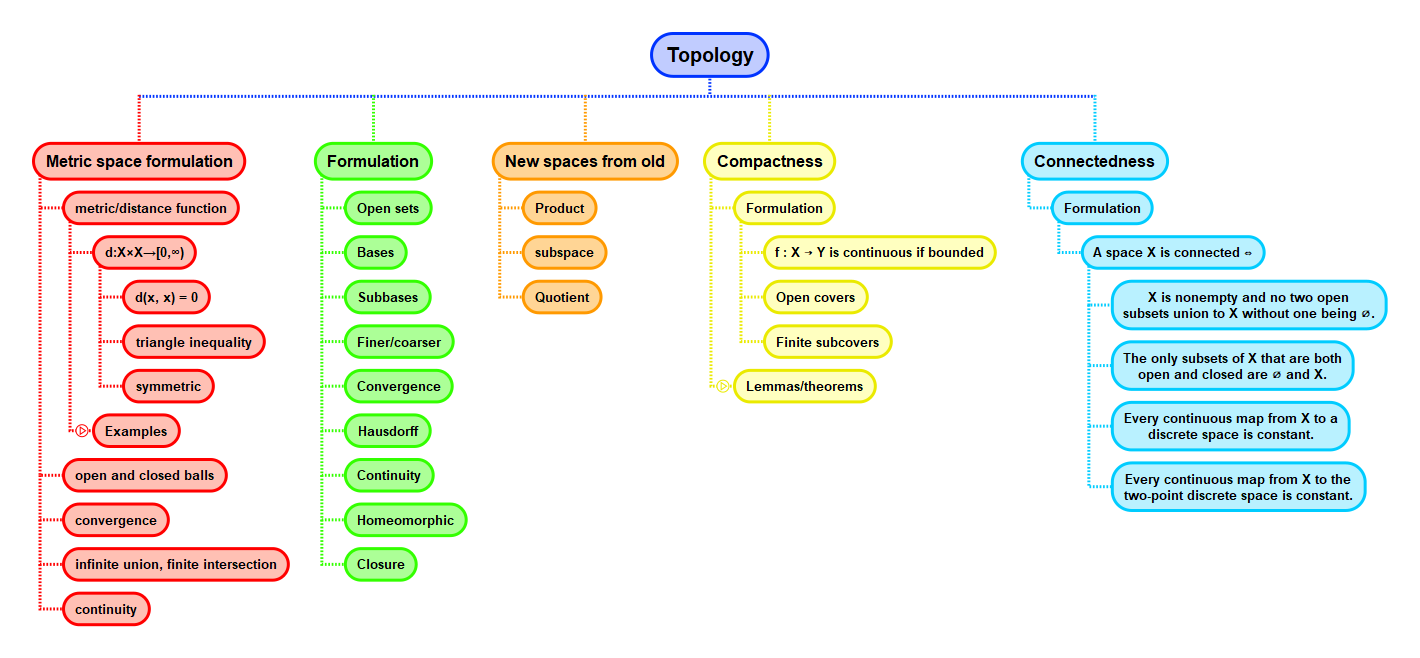
Math and science::Topology

Metric space. Unions and intersections of open sets

  • An arbitrary union of open subsets is open.
  • A finite intersection of open subsets is open.
  • Special cases: \( \emptyset \) and \( X \) are both open and closed.

Lemma. Union and intersection of open sets

Let \( X \) be a metric space.

  • Let \( (U_i)_{i \in I} \) be a family (finite or not) of open subsets of \( X \). Then \( \bigcup_{i\in I} U_i \) is also open in X.
  • Let \( U_1 \) and \( U_2 \) be open subsets of \( X \). Then \( U_1 \cap U_2 \) is also open in X.
  • Special cases \( \emptyset \) and \( X \) are open also.


The mirror statements for closed sets are as follows.

Lemma. Union and intersection of closed subsets

Let \( X \) be a metric space.

  • Let \( V_1 \) and \( V_2 \) be closed subsets of \( X \). Then \( V_1 \cup V_2 \) is also closed in X.
  • Let \( (V_i)_{i \in I} \) be a family (finite or not) of closed subsets of \( X \). Then \( \bigcap_{i\in I} V_i \) is also open in X.

Special cases \( \emptyset \) and \( X \) are also closed.


Context