Finer and coarser topologies
We say that one topology \( \mathcal{T} \) on \( X \) is finer than another topology \( \mathcal{T}' \) on \( X \) iff every member of \( \mathcal{T}' \) is a member of \( \mathcal{T} \). \( \mathcal{T}' \) is said to be coarser than \( \mathcal{T} \).
Stronger and weaker are alternative terminology for finer and coarser.
\( \mathcal{T} \) is strictly finer iff \( \mathcal{T}' \) is a proper subset.
Symbolically,
- \( \mathcal{T} \) is finer than \( \mathcal{T}' \) ⟺ \( \mathcal{T}' \subseteq \mathcal{T} \).
- \( \mathcal{T} \) is strictly finer than \( \mathcal{T}' \) ⟺ \( \mathcal{T}' \subset \mathcal{T} \).
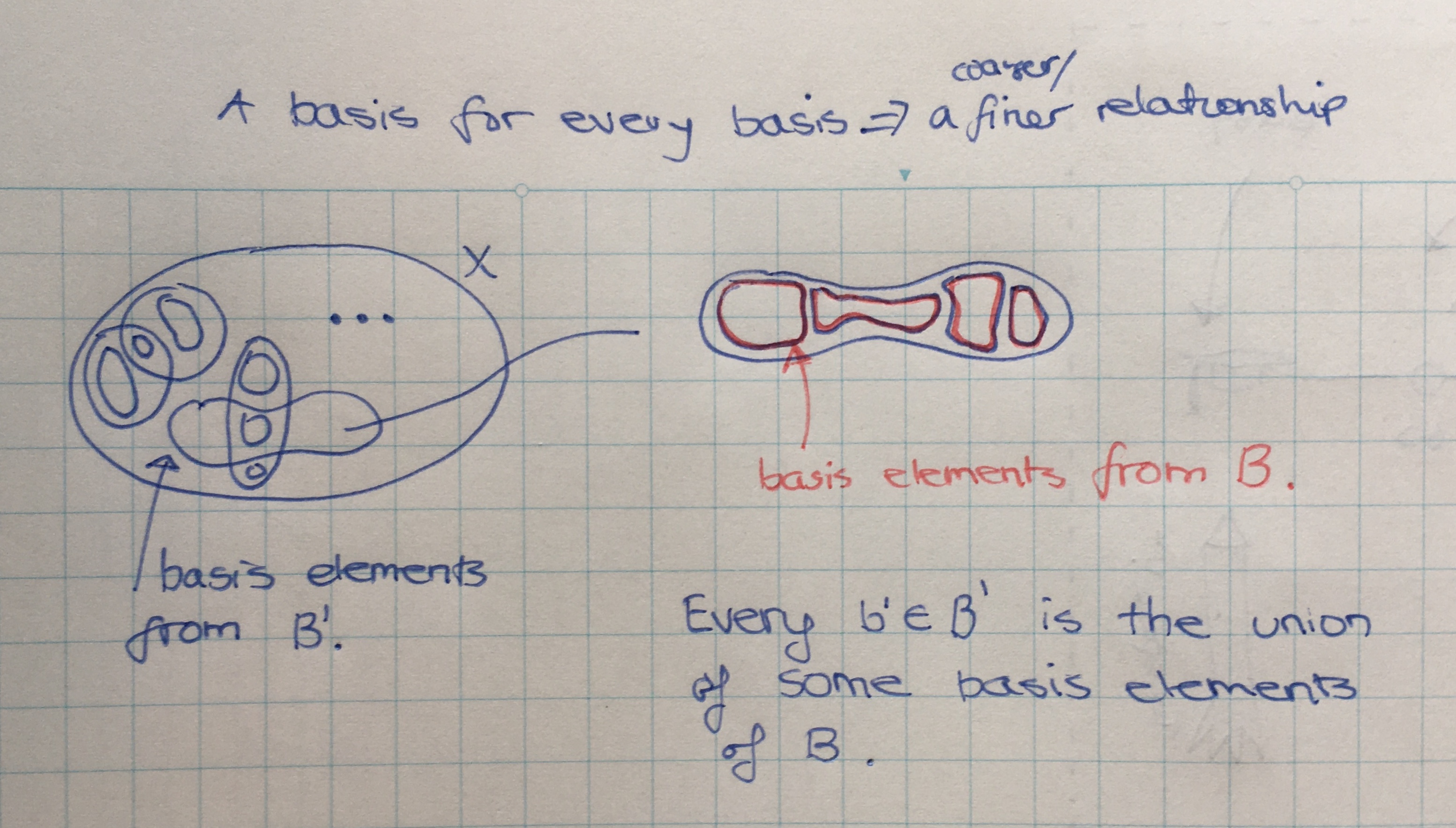
Lemma. A basis for every basis.
Let \( X \) be a set. Let \( \mathcal{T} \) and \( \mathcal{T}' \) be topologies on \( X \) with bases \( \mathscr{B} \) and \( \mathscr{B}' \) respectively. Then \( \mathcal{T} \) is finer than \( \mathcal{T}' \) iff
for each \( x \in X \) and each basis element \( B' \in \mathscr{B'} \) containing \( x \), there is a basis element \( B \in \mathscr{B} \) such that \( x \in B \subseteq B' \).
It should be easy to prove this. Refer to Munkres for a proof example.
By this lemma, it can be seen how a topology induced by one metric can be equivalent to a topology induced by another.
A basis for every basis: alternative perspective
I think a better way of phasing the second part of the iff relationship is to say: every \( b' \in \mathscr{B'} \) can be expressed as a union of elements \( b \in \mathscr{B} \).
Example
For a set \( X \), the discrete topology is the finest topology while the indiscrete topology is the coarsest topology.
Context