Hausdorff spaces
Most interesting topological spaces are Hausdorff. Hausdorffness is identified as being the second separation condition. The first condition, T1 is a sub-requirement of T2 (Housdorff), so it is useful to keep it in mind when thinking about the Hausdorff condition.
T1
A topological space \( X \) is said to be \( T_1 \) iff every one-element subset of \( X \) is closed.
Now for Hausdorff.
Hausdorff
A topological space \( X \) is Hausdorff (or \( T_2 \)) iff for every distinct \( x, y \in X \), there exists disjoint neighbourhoods of \( x \) and \( y \).
Lemma. Every Hausdorff space is \( T_1 \).
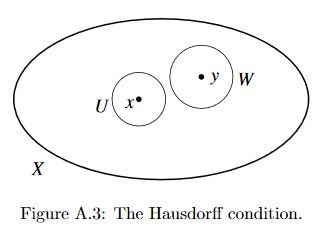
Slightly more precise wording of the Hausdorff condition:
A topological space \( X \) is Hausdorff (or \( T_2 \)) iff for every \( x, y \in X \) such that \( x \ne y \), there exists disjoint open sets \( U, W \) of \( X \) such that \( x \in U \) and \( y \in W \).
Example
Every metrizable space is Hausdorff.
While most interesting spaces are Hausdorff, there are some non-Hausdorff spaces that are important. The Zariski topology is an example.
Context