Sequence convergence
Sequence convergence
Let \( X \) be a topological space, let \( (x_n) \) be a sequence in \( X \) and let \( x_0 \in X \). Then \( (x_n) \) converges to \( x_0 \) iff for every neighbourhood \( U \) of \( x_0 \) there is an \( N \ge 1 \) such that for every \( n \ge N \), \( x_n \in U \).
In other words, every neighbourhood of the point to which a sequence converges must contain the whole tail end of the sequences starting from some arbitrary point in the sequence.
It is a good exercise to check that this definition carries the expected meaning for metric spaces.
Example
Sequences in Hausdorff spaces
A common demonstration of the importance of Hausdorff spaces:
Let \( X \) be a Hausdorff topological space. Then each sequence in \( X \) converges to at most one point.
Another good proof exercise.
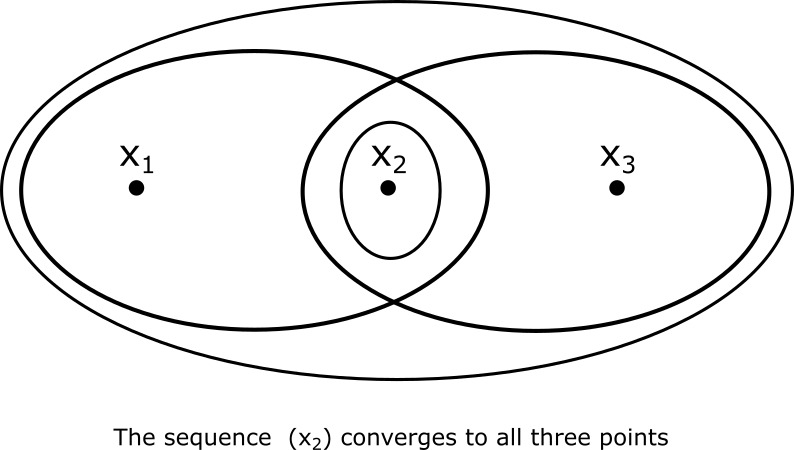
Multiple convergence
An example where we get multiple convergence:
Context