Continuous maps
Continuous maps
Let \( X \) and \( Y \) be topological spaces. A function \( f : X \to Y \) is continuous iff for every open subset \( U \) of \( Y \), the preimage \( f^{-1}U \) is open in \( X \).
In short, continuity means that the preimage of an open set is open.
Some results
Continuous maps preserve convergence of sequences.
Let \( f : X \to Y \) be a continuous map, and let \( (x_n) \) be a sequence in \( X \) converging to \( x \in X \); then the sequence \( (f(x_n)) \) in \( Y \) converges to \( f(x) \in Y \).
In metric spaces this lemma is an if and only if statement, whereas for topological spaces we are restricted to only the forward implication above; it is possible to construct discontinuous maps of topological spaces that, nevertheless, preserve convergence of sequences.
The composite of continuous maps is continuous.
The inverse of a continuous bijection need not be continuous. Details below.
Munkres presents three statements that are equivalent to stating that a function is continuous:
Continuity equivalences
Let \( X \) and \( Y \) be topological spaces and let \( f : X \to Y \) be a function. The the following are equivalent:
- \( f \) is continuous.
- For every subset \( A \) of \( X \), one has \( f(\bar{A}) \subseteq \overline{f(A)} \).
- For every closed set \( B \) of \( Y \), the set \( f^{-1}(B) \) is closed in \( X \).
- For each \( x \in X \) and each neighbourhood \( V \) of \( f(x) \), there is a a neighbourhood \( U \) of \( x \) such that \( f(U) \subseteq V \).
Continuous maps preserve convergence, proof.
The sequence \( (x_n) \) in \( X \) converges to \( \lim_{n \to \infty} x_n \). Any neighbourhood \( B \subseteq Y \) of \( f(\lim_{n \to \infty} x_n) \) has an open pre-image \( A \subseteq X \) that is a neighbourhood of \( \lim_{n \to \infty} x_n \). As \( A \) is a neighbourhood of the limit of the sequence, it must fully contain some tail of the sequence (\( x_n \) for all \( n \ge N \) for some \( N > 0 \)). The image of this tail must fit within \( B \). And so, \( B \) contains a tail of \( (f(x_n))_n \). This is sufficient to conclude that \( \lim_{n \to \infty} f(x_n) \) converges to \( f(\lim_{n \to \infty} x_n) \).
The 4 equivalent statements for continuity
Some remarks about these equivalences:
- #3 implies that continuity could have been defined in terms of closed sets, inplace of opensets; more support that closedness is of equal fundamentalness to openness.
- #4 is the form in which continuity is defined for metric spaces! Just replace notions of neighbourhoods with open ε-balls.
- #2 is presented later on in Leinster's notes. In words it is saying that a sufficient and necessary requirement for a function \( f \) to be continuous is that \( f \) must map points just outside of any set \( A \) to points only just outside \( fA \).
- #2 can be unfolded (and a little bit of causality injected) to say:
no open set in \( X \) can help intersecting \( A \) when containing \( x \) ⟺ no open set in \( Y \) can help intersecting \( fA \) when containing \( f(x) \).
Warning regarding inverse
The inverse of a continuous bijection need not be continuous.
An easy way of constructing an example is to consider continuous maps to a set with the discrete topology. For example, the identity map \( i : (\mathbb{R}, \text{discrete topology}) \to (\mathbb{R}, \text{standard topology}) \) is continuous, but the inverse, \( \) \( i^{-1} : (\mathbb{R}, \text{standard topology}) \to (\mathbb{R}, \text{discrete topology}) \) is not continuous.
Naming: function, map, mapping
'Function', 'map' and 'mapping' usually mean the same thing, but in practice, people tend to talk about 'continuous maps' between topological spaces, rather than 'continuous functions'.
It is worth checking that this notion of continuity is compatible with that defined for metric spaces.
Essence of continuity #1
Continuity in terms of open sets can imagined as a test-response: choose any open set surrounding a point in the image of the continuous function and continuity can assert the existance of a "matching" open set in the domain that contains the pre-image of that point. "Matching" here means that the set in the domain is a pre-image of the set in the co-domain.
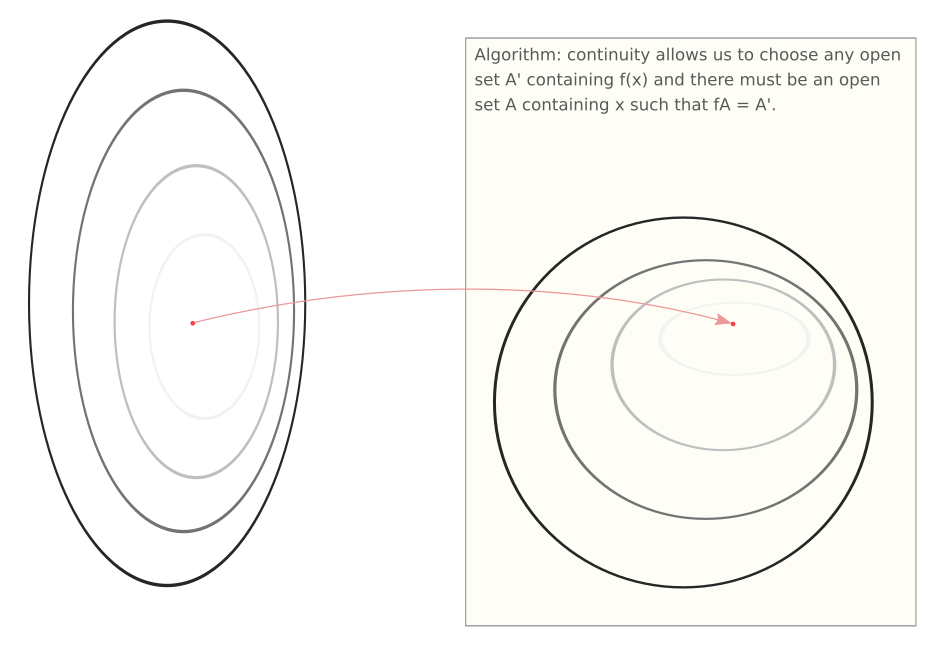
Then note that any open set around a point contains all tails of sequences approaching that point: the open set around a point \( f(x_0) \) in the co-domain contains all sequences that approach \( f(x_0) \), this open set has an open pre-image that must contain all sequences that approach \( x_0 \). There is containment of infinite sequences through the mapping.
Essence of continuity #2
Here we try to view continuity in the forward direction through a function, rather than by going backwards by going through it's image.
In a metric space, a function \( f : X \to Y \) is continuous if it maps nearby points to nearby points, which can be expressed as:
Consider now the idea of closures. For a point \( x \), it is in the closure of a set \( S \subset X \) iff there is a sequence of points in \( S \) that converges to \( x \). With this in mind, we can rewrite the above condition for continuity as:
This is the #2 equivalent form for topological continuity and might feel more familiar by how it seems closer to the idea of continuity in metric spaces.
Example
Mapping from a discrete topology
Any map from a set with a discrete topology is always continuous, as any element of such a topology is always both open and closed.
Mapping to an indiscrete topology
Any map to set with an indiscrete topology is always continuous, as the only two elements in the codomain (full set and empty set) must map to the full set and empty set of the domain. All four of which are both open and closed.
Identity map
Let \( \mathcal{T} \) and \( \mathcal{T}' \) be two different topologies on the same set \( X \). The 'identity' map \( i : (X, \mathcal{T}) \to (x, \mathcal{T}') \), defined by \( i(x) = x \), is continuous iff the codomain \( \mathcal{T}' \) is finer than the domain \( \mathcal{T} \) ( every member of \( \mathcal{T}' \) is also a member of \( \mathcal{T} \) ).
Context