Math and science::Topology

Compactness. Motivation

What would we have to assume about a topological space $X$ in order to prove that every continuous map $f : X \to R$ is bounded?

Reasoning summary

Condensed version.

What is the definition of being bounded?
What are some cases where we know functions are bounded?
The most basic case: the domain is finite.
Can we generalize this?
A little more general:
For a given $f$ , the domain can be covered by a finite collection of subsets, each of which has an image that is bounded.
This is restricted to a given $f$ . Can we generalize?
Every continuous $f$ induces a neighbourhood around each $x \in X$ , and $f$ will be bounded for each of these neigbourhoods. (Remember, the codomain is $R$ ).
So, by the definition of continuity, we have a cover where each subset is bounded.
Sadly, this set of neighbourhoods could be infinite.
Thus we arrive at our requirement: every open cover must have a finite subcover.
Which means, every continuous $f$ will induce an arbitrary open cover on $X$ (by continuity), and we impose that this cover has a finite subcover.

Reasoning steps

The though chain in full.

1. Define bounded

For the single dimension case, the following are equivalent statements regarding a function $f : X \to R$ :

$f$ is bounded.
$f X$ is bounded.
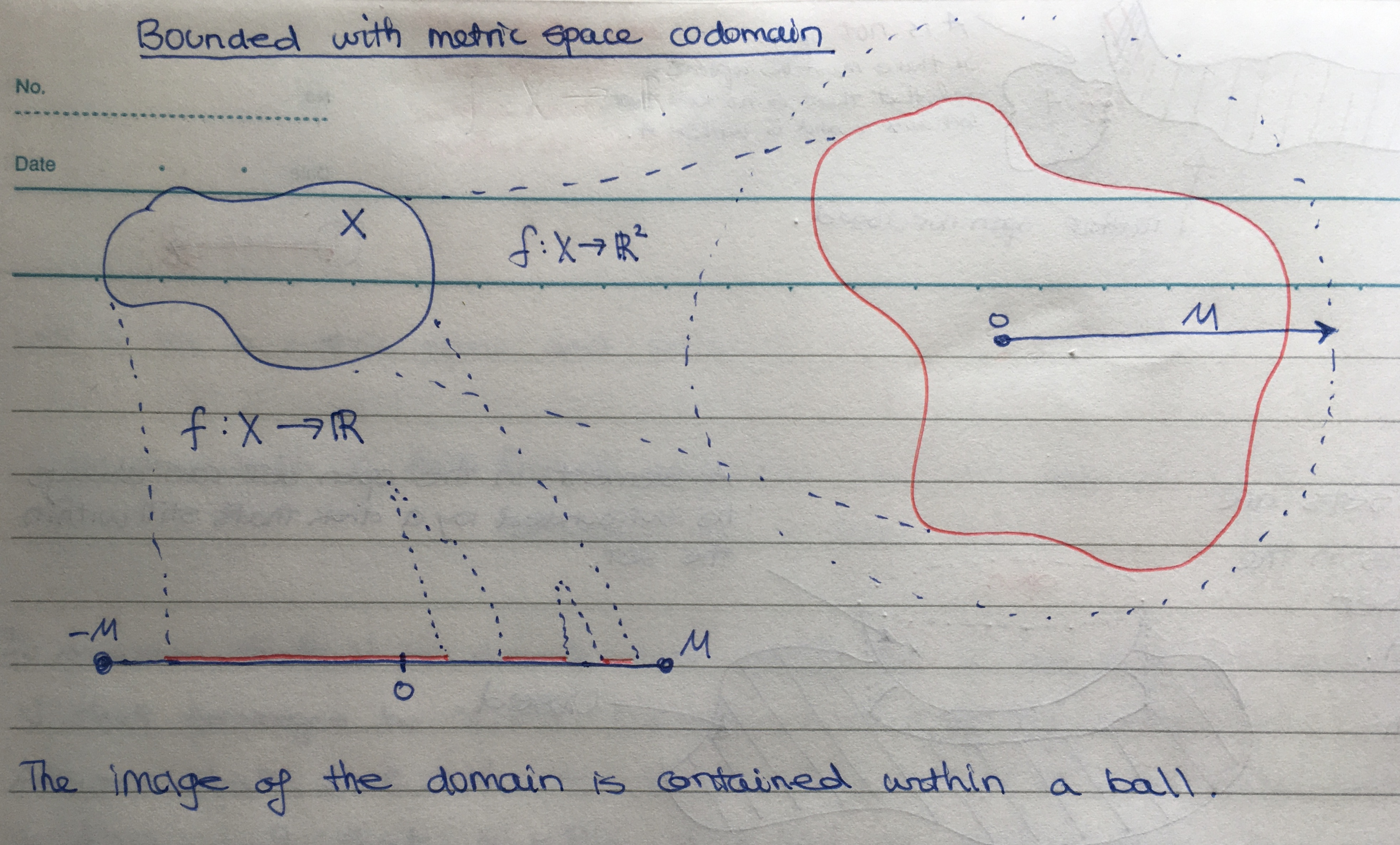
There exists an $M \geq 0$ such that for all $y \in f X$ , $| y | \leq M$ .
There exists an $M \geq 0$ such that for all $x \in X$ , $| f (x) | \leq M$ .
As $R$ is a metric space, we can phrase #3 with ε-balls: there is an $B (0, M)$ for some $M \geq 0$ such that $f X \subseteq B (0, M)$ .

2. Functions with finite domain are bounded

If $X$ is finite, then any function $f : X \to R$ (continuous or not) is bounded, since we can take $M = m a x_{x \in X} | f (x) |$ . max over a finite set of real numbers is a real number.

3. $X$ covered by finite bounded subsets

If the domain $X$ can be expressed as a finite union of subsets $(A_{j})_{j \in J}$ such that a function $f : X \to R$ is bounded on each individual $A_{j}$ , then $f$ itself must be bounded. Why? Well, we can choose for each $j \in J$ some $M_{j} \geq 0$ such that for all $x \in A_{j}, | f (x) | \leq M_{j}$ . Then the maximum of these, $M = max_{j \in J} M_{j}$ bounds the whole of $f X$ .

Now the question becomes, given a set $X$ , how can we express it as a union of bounded sets.

4. Locally bounded near every $x \in X$

A continuous function need not be bounded, but it is 'locally bounded' in the following sense.

Metric space, $X$: Let $x \in X$ . There is some $δ_{x} > 0$ such that $B (x, δ_{x})$ is a subset of $f^{- 1} (f (x) - 1, f (x) + 1)$ , the latter being an open neighbourhood of $x$ .
The same idea for a topological space, $X$ , and function $f : X \to R$: Let $x \in X$ . The set $U_{x} = f^{- 1} (f (x) - 1, f (x) + 1)$ is an open neighbourhood of $x$ and satisfies $f U_{x} \subseteq (f (x) - 1, f (x) + 1)$ .

In both of these cases, $f$ is bounded by $f (x) + 1$ when restricted to $B (x, δ_{x})$ and $U_{x}$ respectively. So each $x \in X$ has a neighbourhood on which $f$ is bounded.

Trying to utilize this idea to cover $X$ with bounded subsets runs up against issues of infinite sets.

5. The maximum of an infinite set

We know that for each $x \in X$ , there is a neighbourhood $U_{x}$ on which the continuous function $f$ is bounded, with $| f (u) | \leq M_{x}$ for all $u \in U_{x}$ . The subsets $(U_{x})_{x \in X}$ cover $X$ , so why not use $M = max_{x \in X} M_{x}$ as the bounds for $f$ ? The trouble is, this maximum might not be a well-defined real number, since $X$ is infinite.

6. Impose a finite cover requirement

Presuppose that it was possible to cover $X$ with only finitely many of the sets $U_{x}$ . If $Z \subseteq X$ was a finite set such that the neighbourhoods $(U_{x})_{x \in Z}$ covered $X$ , then we could legitimately set $M = max_{z \in Z} M_{z}$ .

So, in order to be able to assert that all continuous maps $X \to R$ be continuous, we have needed to assume that there is a finite set of open subsets that cover $X$ . This is exactly what the definition of compact entails. The definition is copied below.

Cover

Let $X$ be a topological space. A cover of $X$ is a family $(U_{i})_{i \in I}$ of subsets of $X$ such that $⋃_{i \in I} U_{i} = X$ . It is finite iff the indexing set $I$ is finite, and open iff $U_{i}$ is open for each $i \in I$ .

Given a cover $(U_{i})_{i \in I}$ and $J \subseteq I$ , we say that $(U_{j})_{j \in J}$ is a subcover of $(U_{i})_{i \in I}$ if it is itself a cover of $X$ .

Finally, we arrive at our definition for compact.

Compact

A topological space $X$ is compact iff every open cover of $X$ has a finite subcover.

We have achieved boundedness

If we take any continuous function $X \to Y \subseteq R^{n}$ , where $X$ is compact, $f X$ must have a finite open cover, as $X$ has a finite open cover. Consequently, $f X$ must be bounded: $f X \subseteq [- M, M]^{n}$ , where $M$ is a maximum of the bounds of the finite covers of $f X$ .

Context

22.05.2020