\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)

Compactness. Motivation

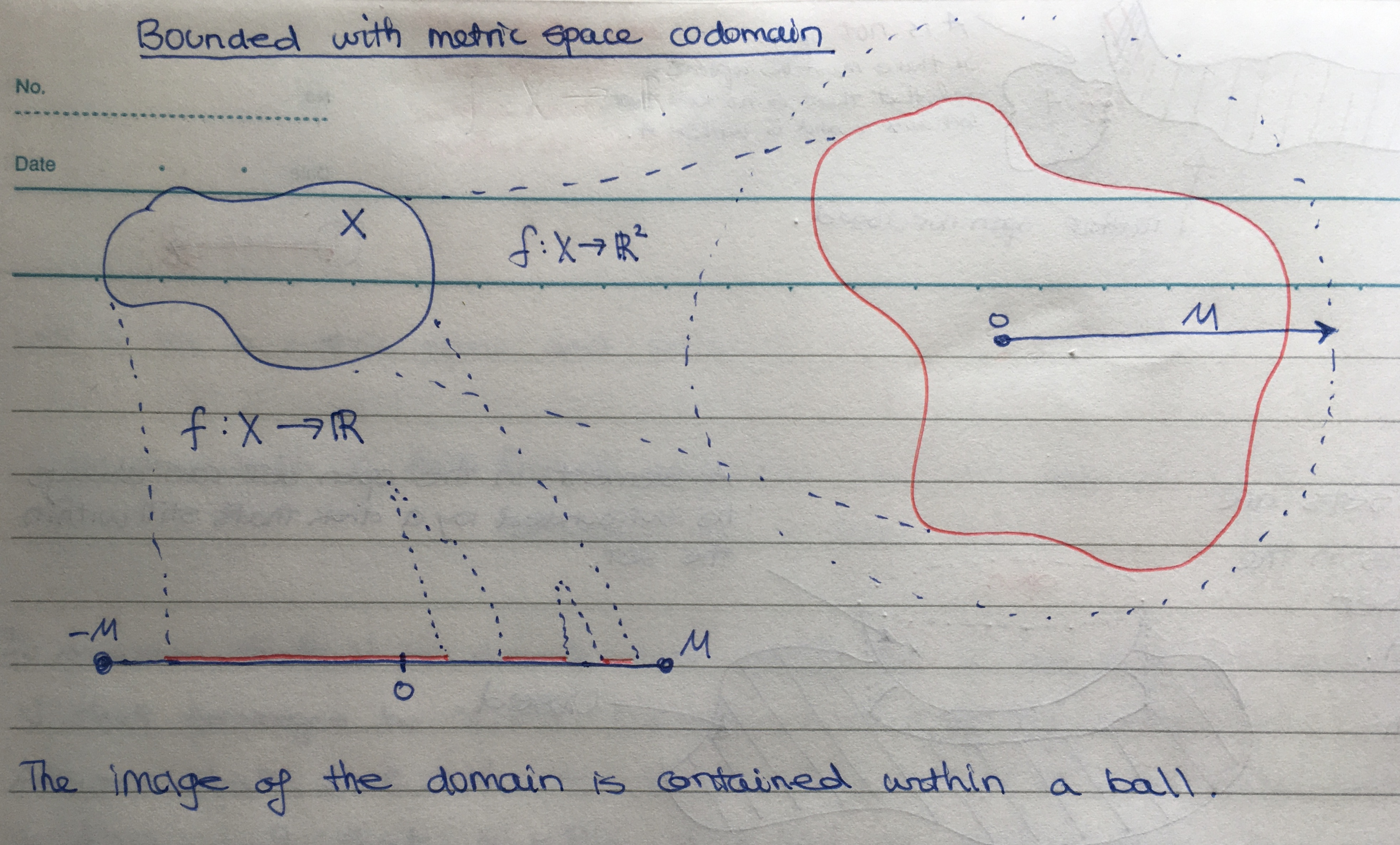
What would we have to assume about a topological space \( X \) in order to prove that every continuous map \( f : X \to \mathbb{R} \) is bounded?

Reasoning summary

Condensed version.

• What is the definition of being bounded?
• What are some cases where we know functions are bounded?
• The most basic case: the domain is [...].
• Can we generalize this?
• A little more general:
  For a given \( f \), the domain can be covered by a [...], each of which has an image that is bounded.
• This is restricted to a given \( f \). Can we generalize?
• Every continuous \( f \) induces a neighbourhood around each \( x \in X \), and \( f \) will be bounded for each of these neigbourhoods. (Remember, the codomain is \( \mathbb{R} \)).
• So, by the definition of continuity, we have a cover where each subset is bounded.
• Sadly, this set of neighbourhoods could be [...].
• Thus we arrive at our requirement: every open cover must have [...].
• Which means, every continuous \( f \) will induce an arbitrary open cover on \( X \) (by [definition of what?]), and we impose that this cover has a finite subcover.