Compactness
Compact sets can be thought of as a generalization of closed sets. See the reverse side for a justification.
There are multiple ways of formulating compactness, with some being more intuitive than others.
There are 3 formulations that are particularly important.
1. Compactness, in terms of sequences in \( \mathbb{R} \).
A set \( K \subset \mathbb{R} \) is compact iff every sequence in \( K \) has a subsequences that converges to a limit that is also in \( K \).
What is the topological generalization of this definition?
The most basic example of such a closed set in \( \mathbb{R} \) is a closed interval.
Bolzano-Weierstrass's theorem connects the first and second formulations.
2. Compactness, in terms of closed, bounded sets.
A set \( K \subset \mathbb{R}^n \) is compact iff it is closed and bounded.
The next formulation is the most general of the three, graduating to the topic of topology. It uses the idea of a cover and a subcover.
Cover
Let \( X \) be a topological space. A cover of \( X \) is a family \( (U_i)_{i \in I} \) of subsets of \( X \) such that \( \bigcup_{i \in I} U_i = X \). It is finite iff the indexing set \( I \) is finite, and open iff \( U_i \) is open for each \( i \in I \).
Given a cover \( (U_i)_{i \in I} \) and \( J \subseteq I \), we say that \( (U_j)_{j \in J} \) is a subcover of \( (U_i)_{i \in I} \) if it is itself a cover of \( X \).
3. Compactness, in terms of covers.
A topological space \( X \) is compact iff every open cover of \( X \) has a finite subcover.
What is the theorem that connects these three formulations of compactness?
Heine-Borel theorem
The Heine-Borel theorem is precicely the statement that ties these three notions of compactness together. [Hmm... actually, I think the Heine-Borel theorem might only cover the equivalence of the first two].
Heine-Borel theorem
Let \( K \) be a subset of \( \mathbb{R} \). The following three statements are equivalent:
- \( K \) is compact.
- \( K \) is closed and bounded.
- Every open cover of \( K \) has a finite subcover.
Proof 1: #2 \(\implies\) #3
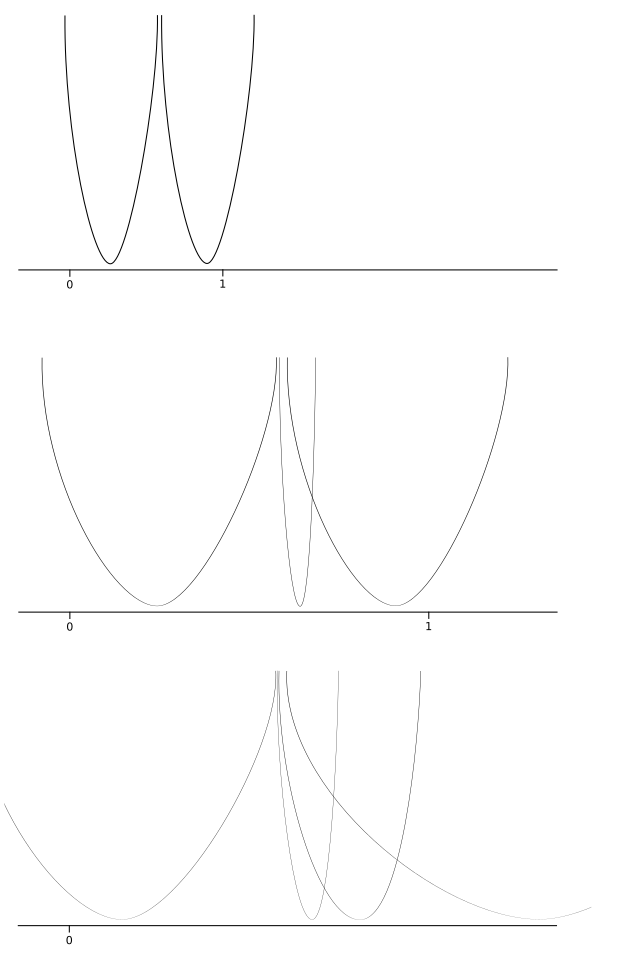
A MathExchange answer does a good job of motivating intuition as to why a closed interval must always have a finite subcover. Below is a screenshot of the proof (that any cover of \([0, 1]\) has a finite subcover).

Proof 1 essence
If prooving by contradiction, we must be able to zoom in on an ever narrower closed sub-interval of \([0, 1]\) that requires an infinite cover. As the intervals are closed, their intersection is not empty, but a point. This point must be in an open set of the cover, but this open set must cover at least some of the intervals that we zoomed in on.
Infinite open covers can occur when covering next to and edge. But if we need to cover the edge, then the open set that covers the edge will also cover the tail of our infinite cover.
The essence of compactness
Abbott on p97 mentions this about compact sets and closed intervals:
There may be a temptation to consider closed intervals as being a kind of standard archetype for compact sets, but this is misleading. The structure of compact sets can be much more intricate and interesting. For instance, one implication of Theorem 3.3.4 is that the Cantor set is compact. It is more useful to think of compact sets as generalizations of closed intervals. When ever a fact involving closed intervals is true, it is often the case that the same result holds when we replace “closed interval” with “compact set.” As an example, let’s experiment with the Nested Interval Property proved in the first chapter...
He then goes on to prove a version of the nested closed interval property, but with compact sets replacing closed intervals:
If \( K_1 \supseteq K_2 \supseteq K_3 \supseteq K_4 \supseteq ... \) is a nested sequence of nonempty compact sets, then the intersection \( \cap_{n=1}^{\infty} K_n \) is not empty.
Even more content...this whole section from Abbott is good to re-read.


Some phrasing that might help reading the above excerpt
The watershed case is covering a sequence of points in a set of reals (or rationals) with ever smaller open sets. Think of a sequence from the set that approaches some limit. What if the set (and thus the sequence) is bounded? What if the sequence approaches a limit within the set (i.e. think closed sets)? All points of the sequence has some wriggle-room; in other words, can be covered by an open subset. If a finite-cover is possible, then the sequence can't approach a limit outside of the set.
Other links
There are some interesting descriptions on this Math Exchange page.
Context