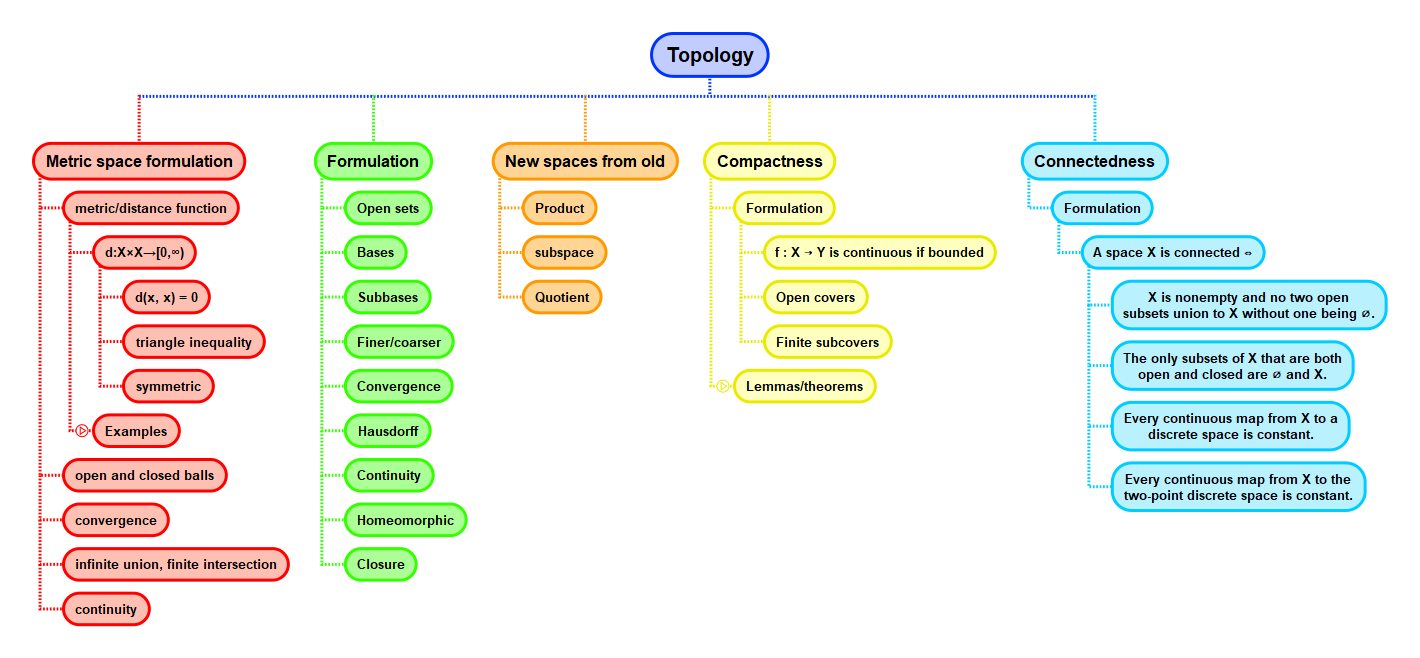
Math and science::Topology
Connectedness, compactness and some fundamental theorems of calculus
The following three theorems in calculus, theorems about functions from and to the reals, have generalizations in topology.
- Intermediate value theorem
- If \( f : [a, b] \to \mathbb{R} \) is continuous, and if \( r \) is a real number between \( f(a) \) and \( f(b) \), then there exists an element \( c \in [a, b] \) such that \( f(c) = r \).
- Maximum value theorem
- If \( f : [a, b] \to \mathbb{R} \) is continuous, then there exists an element \( c \in [a, b] \) such that \( f(x) \le f(c) \) for every \( x \in [a, b] \).
- Uniform continuity theorem
- If \( f : [a, b] \to \mathbb{R} \) is continuous, then for every \( \varepsilon > 0 \) there exists a \( \delta > 0 \) such that \( |f(x_1) - f(x_2)| < \varepsilon \) for every \( x_1, x_2 \in [a, b] \) for which \( |x_1 - x_2| < \delta \).
Applications in Calculus
- The intermediate value theorem is used for constructing inverse functions, such as \( \sqrt[3]{x} \) and \( \arcsin(x) \).
- The maximum value theorem is used to prove the mean value theorem for derivatives, which in turn is used to prove the two fundamental theorems of calculus.
- The uniform continuity theorem is used for proving that every continuous function is integrable.
What is the concept in question: functions vs sets?
The three theorems can be considered to be describing facts about continuous functions; but shifting one's focus, one can view them as describing the nature of the closed interval \( [a, b] \subset \mathbb{R} \).
As topological properties
The topological property of the space \( [a, b] \) on which the intermediate value theorem depends is the topological property called connectedness.
The property which the maximum value theorem and the uniform continuity theorem depend on is called compactness.
Both of these properties are fundamental to areas beyond calculus; they are fundamental to almost any area which can be represented in topology.
Context
Source
Munkresp145
