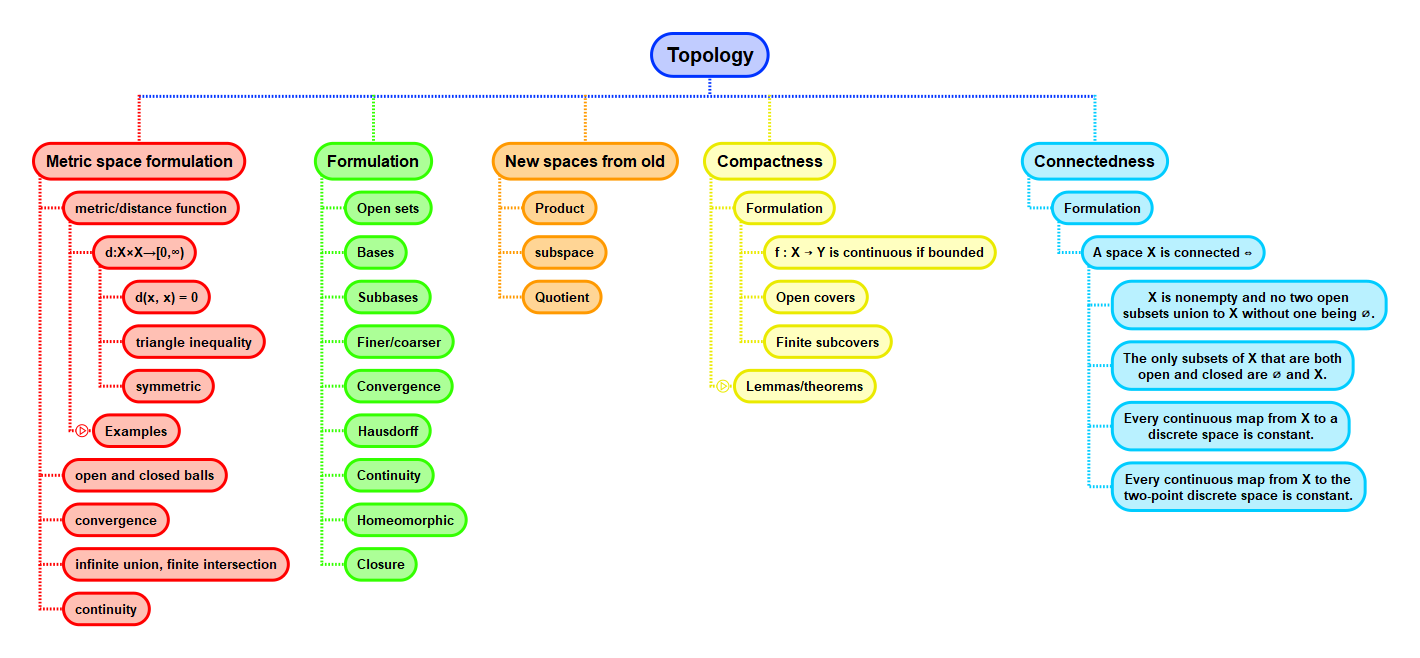
Connectedness Examples

• $X=\mathbb{R}\setminus \{0\}$ is disconnected, since $(-\mathrm{\infty },0)$ and $(0,\mathrm{\infty })$ are disjoint open subsets of $X$ whose union is $X$.
• The space of rationals numbers $\mathbb{Q}$, topologized as a subspace of $\mathbb{R}$, is disconnected. Consider the pair of open sets $(-\mathrm{\infty },\sqrt{(}2))\cap \mathbb{Q}$ and $(\sqrt{(}2),\mathrm{\infty })\cap \mathbb{Q}$.
• A discrete space with 2 or more points is disconnected. If $X$ is such a space, we can choose an $x_1\in X$ then consider the two open sets $\{x_1\}$ and $X\setminus \{x_1\}$.
• A non-empty indiscrete space is connected.
• An interval topologized as a subspace of $\mathbb{R}$ is connected.
• The space ${\mathbb{R}}^d$ is not necessarily connected nor disconnected—it is connected in the product topology, but not connected in the box topology.
• The letter 'O' is connected. '0' is a quotient of $[0,1]$, the quotient map is continuous and the image of a connected space through a continuous function is connected.
• The collection of connected sets in $\mathbb{R}$ coincide preciesly with the collection of intervals.