\( \newcommand{\matr}[1] {\mathbf{#1}} \newcommand{\vertbar} {\rule[-1ex]{0.5pt}{2.5ex}} \newcommand{\horzbar} {\rule[.5ex]{2.5ex}{0.5pt}} \)
deepdream of a sidewalk
Show Question
\( \newcommand{\cat}[1] {\mathrm{#1}} \newcommand{\catobj}[1] {\operatorname{Obj}(\mathrm{#1})} \newcommand{\cathom}[1] {\operatorname{Hom}_{\cat{#1}}} \newcommand{\multiBetaReduction}[0] {\twoheadrightarrow_{\beta}} \newcommand{\betaReduction}[0] {\rightarrow_{\beta}} \newcommand{\betaEq}[0] {=_{\beta}} \newcommand{\string}[1] {\texttt{"}\mathtt{#1}\texttt{"}} \newcommand{\symbolq}[1] {\texttt{`}\mathtt{#1}\texttt{'}} \)
Math and science::Topology

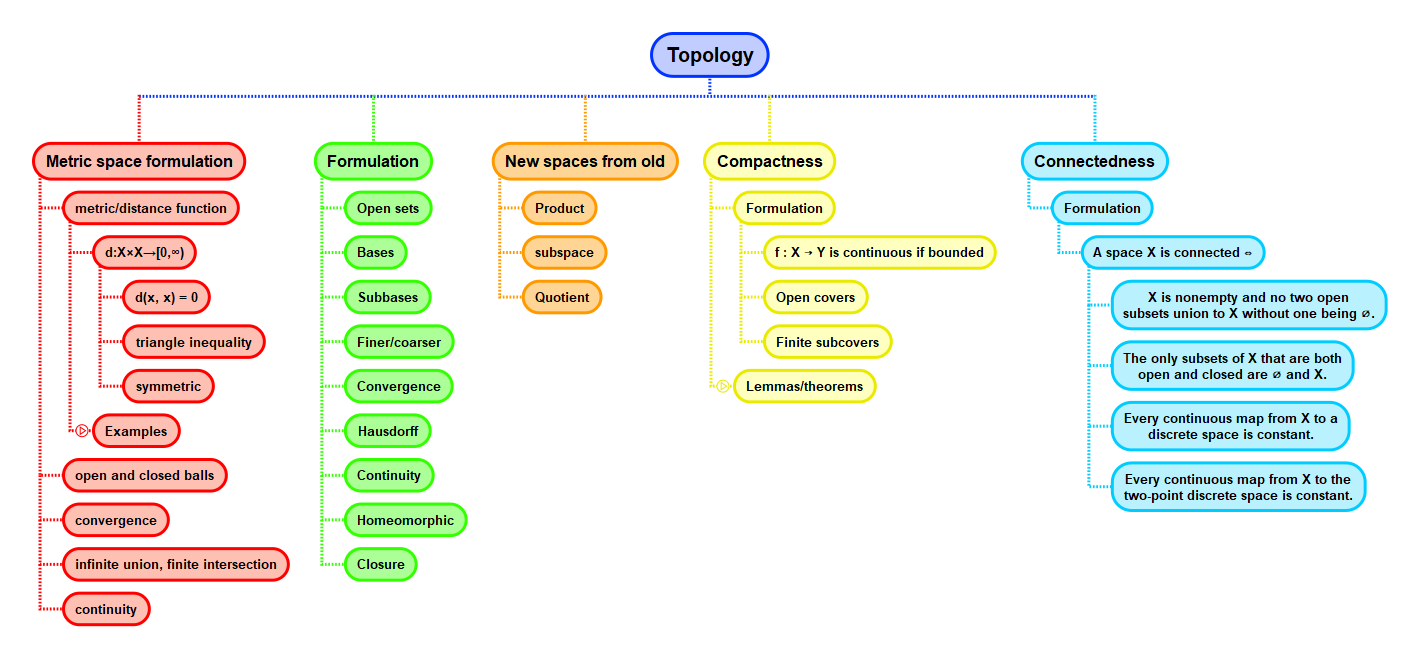
Connectedness. Equivalent formulations

For a nonempty topological space \( X \), the following are equivalent:

  1. \( X \) is connected;
  2. the only subsets that are both open and closed are \( \emptyset \) and \( X \);
  3. every continuous map from \( X \) to a discrete space is constant;
  4. every continuous map from \( X \) to the two-point discrete space is constant.

The 3rd and 4th statement are similar, yet both useful in their own right: the 3rd statement is general and allows progress to be made in a proof when one knows that \( X \) is connected. The 4th is powerful in the reverse direction: simply proving that all continuous maps to the two-point discrete space is constant is enough to show that \( X \) is connected.

Context

Source

Leinster, p 69