Connectedness. 4 lemmas
1. The edge of a connected space
Let \( X \) be a topological space. Let \( A \) and \( B \) be subspaces of \( X \) with \( A \subseteq B \subseteq \operatorname{Cl}(A) \).
If \( A \) is connected, then so is \( B \).
2. An image of a continuous function on a connected space is connected
Let \( f : X \to Y \) be a continuous map of topological spaces. If \( X \) is connected then so is \( fX \).
In particular, any quotient of a connected space is connected.
3. The product of two connected spaces is connected.
4. A space that has an overlapping covering of connected subspaces is connected.
Let \( X \) be a nonempty topological space and \( (A_i)_{i \in I} \) a family of subspaces covering \( X \). Suppose that \( A_i \) is connected for each \( i \in I \) and that \( A_i \cap A_j \neq \emptyset \) for each \( i, j \in I \), then \( X \) is connected.
This lemma says that gluing together overlapping connected spaces produces connected spaces.
1. (\( A \text{ is connected } \implies A \subseteq B \subseteq Cl(A)) \implies B \text { is connected}\)). Proof outline.
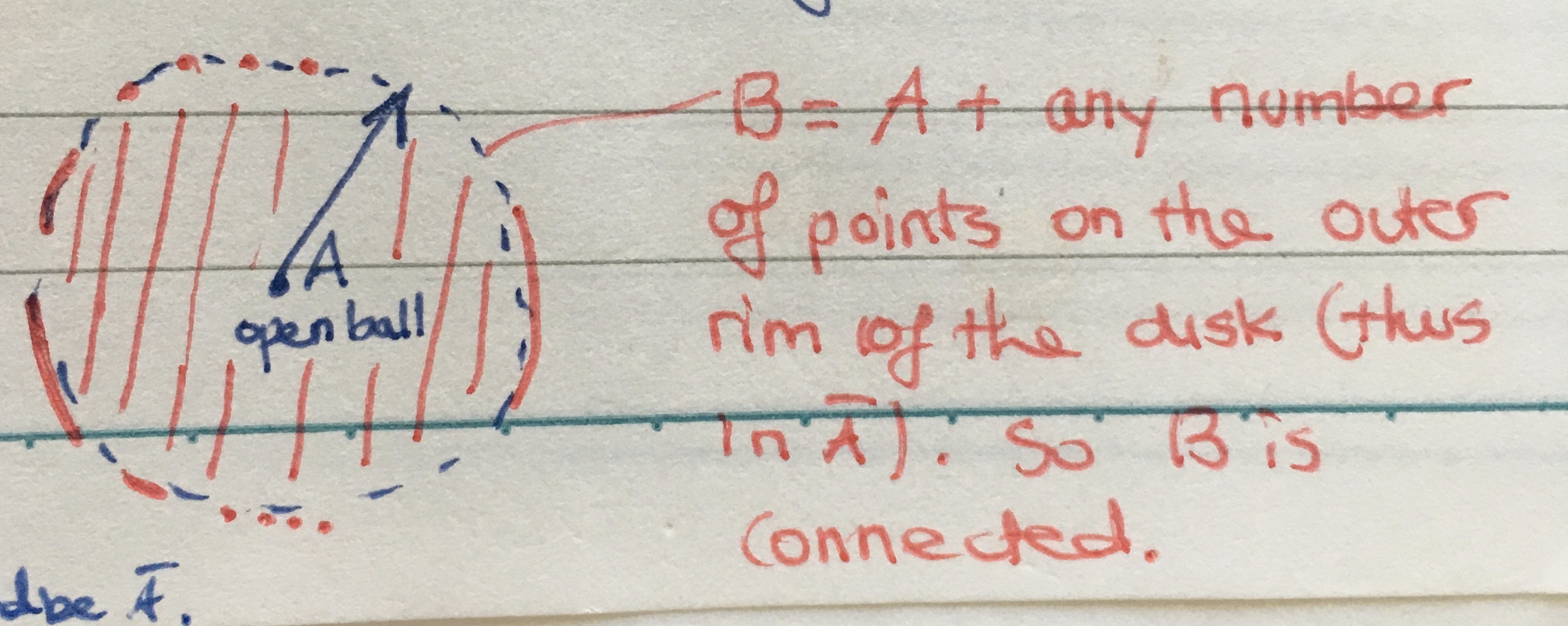
\( B \) is within the smallest closed subset containing \( A \). How could \( B \) be divide into 2 disjoint closed/open sets with \( A \) in one and the rest in another? It can't—if it could, then \( A \) itself would be closed, and thus, it's own closure. Note: \( A \) is connected, so cannot be subdivided to create the pair of open/closed subsets of \( B \).
A good example for visualizing this lemma is to consider \( A \) to be the open unit disk, and for this lemma to represent the inability to create a separation of the closed disk with the open disk contained whollly in one of the sets of the separation.
2. A continuous image of a connected space is connected. Proof outline.
The restricted function \( f : X \to fX \) is surjective, and \( f^{-1}fX = X \). If we can split \( fX \) into two disjoint non-empty open sets, then the pre-image of those sets will be open, disjoint and non-empty in \( X \), and they will union to \( X \). But that is a contradiction, as \( X \) is connected.
3. Product of two connected spaces is connected. Proof outline.
Let \( X \) and \( Y \) be connected spaces, and consider \( X \times Y \).
Two approaches:
- Show that if \( X \times Y \) is not connected, then either \( X \) or \( Y \) cannot be connected. An ability to find a separation of \( X \times Y \) implies that we have found a separation of either \( X \) or \( Y \) or both.
- The approach taken by Leinster is to consider a continuous function \( f : X \times Y \to D \), where \( D \) is a discrete space, and show that \( f \) is a constant function. In the 'Connectedness. Equivalent formulations' card, it was shown that this is necessary and sufficient for \( X \times Y \) to be connected. The demonstration that \( f \) is constant is done by taking two arbitrary points \( t_1, t_2 \in X \times Y \) and considering a 'vertical' slice passing through \( t_1 \) and a 'horizontal' slice passing through \( t_2 \). These slices are homeomorphic to one of \( X \) and \( Y \), so \( f \) must be constant alone both. As the two slices intersect somewhere, \( f \) must be the same constant on each. As the points were arbitrary, this covers the whole space.
4. Union of overlapping connected spaces is connected. Proof.
Let \( f \) be a continuous map from \( X \) to a discrete space \( D \). For each \( i \in I \), we have the continuous map \( f|_{A_i} : A_i \to D \). \( A_i \) is connected, so \( f|_{A_i} \) has a constant value \( d_i \). But for each \( i, j \in I \), we have \( A_i \cap A_j \neq \emptyset \), so \( d_i = d_j \). Hence \( d_i \) is independent of \( i \in I \), so \( f \) is constant, as required.
Example: the letter O is a quotient of \( [0, 1] \), which is connected, so \( O \) is connected. Gluing O to another line segment gives P, which must now also be connected. Gluing on another line segment to give A shows us that A too is connected.
Context